Link: https://leetcode.com/problems/amount-of-time-for-binary-tree-to-be-infected/
Solution:
Intuition
Not much to this problem. We just convert the tree to a graph, find the start node and then perform a BFS.
Note: there is also a very tricky DFS solution that is similar to Diameter of a binary tree…look over it.
Implementation
def time_infected(root, start):
queue = deque()
def dfs(node, parent):
if node is None:
return
if node.val == start:
queue.append((node, 0))
node.parent = parent
dfs(node.left, node)
dfs(node.right, node)
return
dfs(root, None)
visited = set() #or use prev instead to prevent cycles
time = 0
while queue:
node, level = queue.popleft()
if node is None or node.val in visited:
continue
time = level
visited.add(node.val)
queue.append((node.parent, level + 1))
queue.append((node.left, level + 1))
queue.append((node.right, level + 1))
return time
#time: o(n)
#memory: o(n)Visual
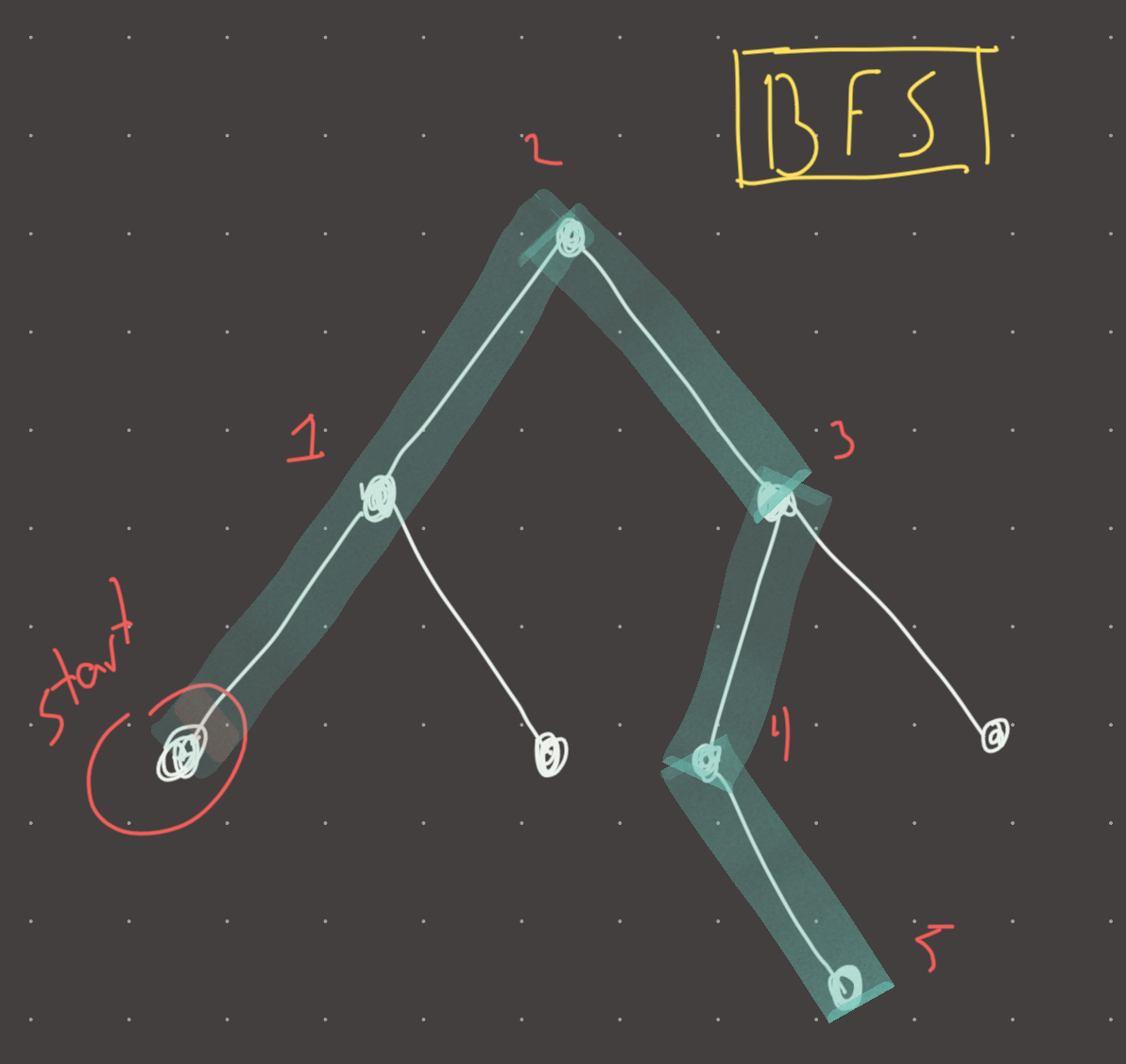
Review 1
BFS is trivial, I still don’t fully understand the DFS solution but essentially you need to count depths differently depending on where the start was found…in other-words its very annoying. Stick to BFS for this problem type.