Link: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/
Solution:
Topics: greedy
Intuition
I initially came up with a very contrived recursive DP solution. In fact, it was so contrived that it was impressive! I essentially mapped it onto an optimal play pattern and still solved it linearly, but could not come up with the greedy o(1) memory solution.
I’m going to do something that I usually don’t do. I will write the implementation first, and discussion will follow.
Implementation
def buy_sell2(prices):
res = 0
for i in range(len(prices)-1):
if prices[i+1] > prices[i]:
res += prices[i+1] - prices[i]
return res
#time: o(n)
#memory: o(1)Look at this code. Why does it work? You would think that there has to be an optimal subsequence right? Why is it the case that if the next number is greater than the current, we can just greedily take the profit? Does it not matter when you buy and when you sell?
Consider the following prices:
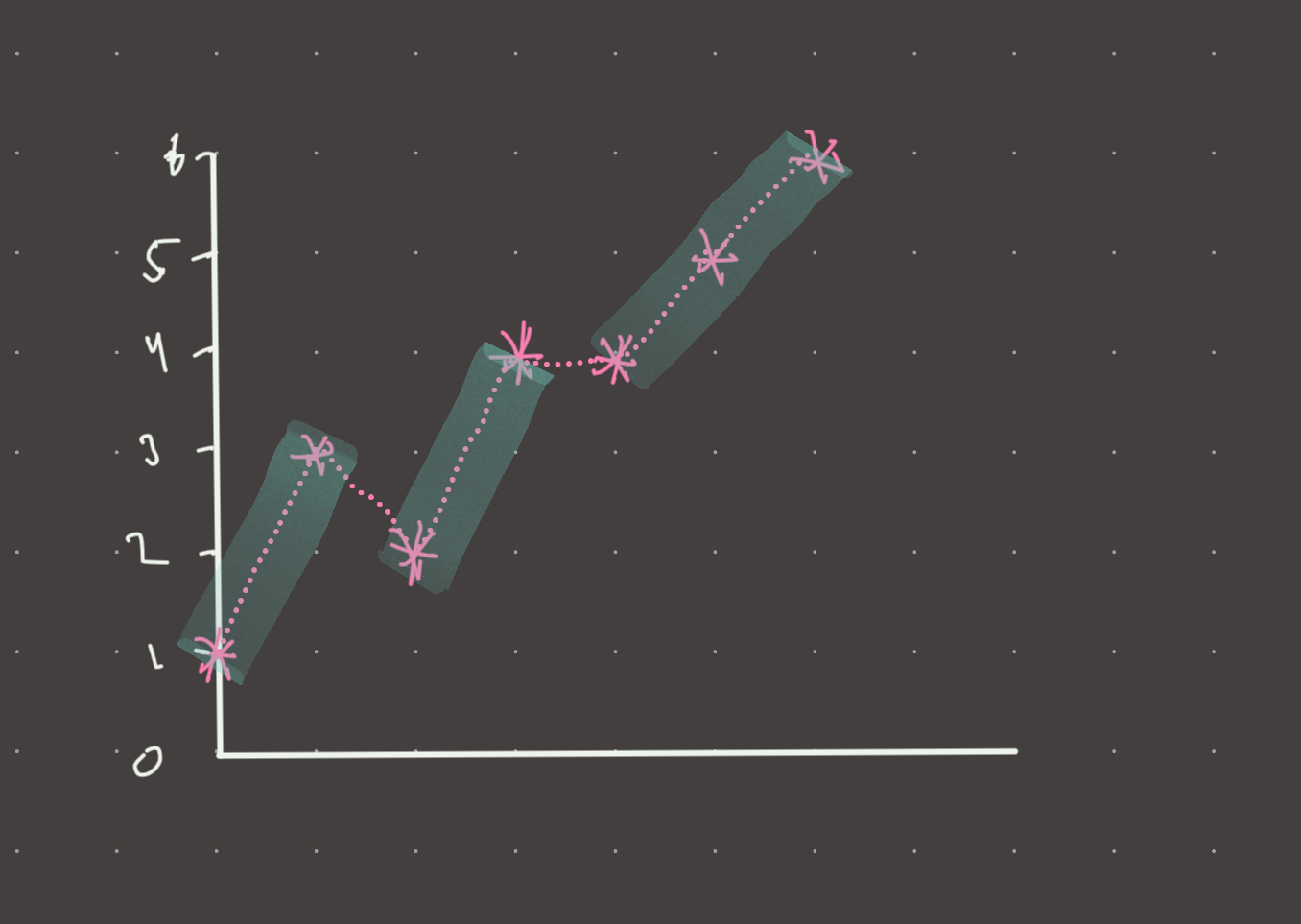
It can be shown that whenever the slope is positive, a profit can be taken. Essentially, if the next day is worth more than today, we take the profit! There is no need to buy on one day and sell on another…we can simply accumulate the profit bit-by bit!
A nice analogy is as follows: If you wanted to track your weight loss over a month, you could weight yourself only twice (first day and last day). Or you could weight yourself every day, and add the difference from the previous day to the total. The result would be the same. This problem is no different.