Boundary of binary tree

Link: https://leetcode.com/problems/boundary-of-binary-tree/

Solution:

Topics: dfs

Intuition
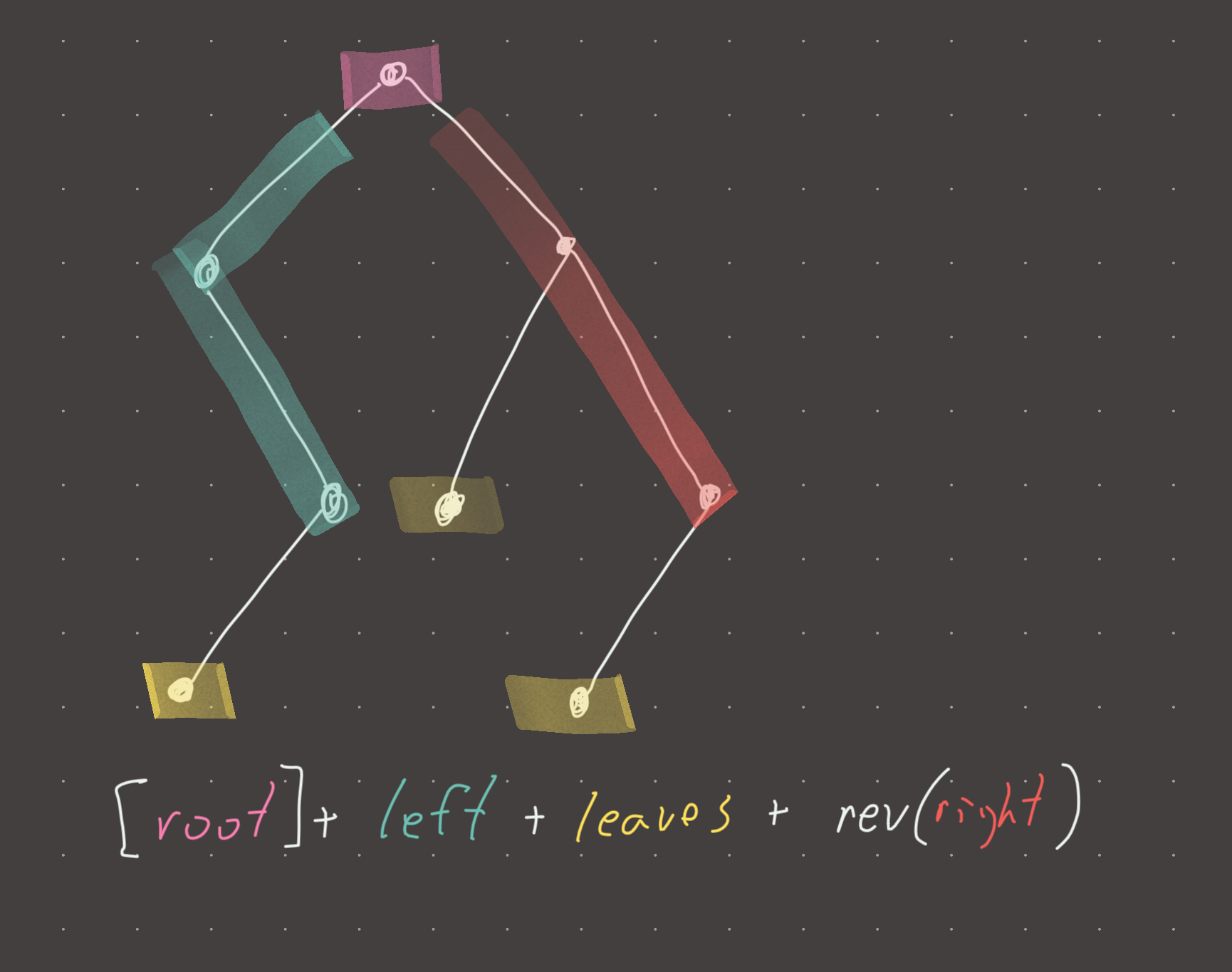
This problem is a lot simpler than it appears. If you read carefully what constitutes a left and right boundary, you realize that its just a log(n) traversal down to the leftmost or rightmost node…storing every node on the way. The leaves can be obtained in the correct order (left first) with an o(n) depth first search.

There are a couple of edge cases. First, we want to make sure that we add the root at the end…this simplifies the logic. Second, we must ensure that we don’t add the leftmost and rightmost leaves twice (easy to miss since we would have already added these nodes in the left/right boundaries).

Implementation

def boundary(root):
	left = []
	def left_dfs(node):
		if not node or not (node.left or node.right):
			return
		left.append(node.val)
		if node.left:
			left_dfs(node.left)
		else:
			left_dfs(node.right)
			
	right = []
	def right_dfs(node):
		if not node or not (node.left or node.right):
			return
		right.append(node.val)
		if node.right:
			right_dfs(node.right)
		else:
			right_dfs(node.left)
 
	leaves = []
	def dfs(node):
		if not node:
			return
		if not node.left and not node.right and node is not root:
			leaves.append(node.val)
		dfs(node.left)
		dfs(node.right)
 
	left_dfs(root.left)
	right_dfs(root.right)
	dfs(root)
 
	return [root.val] + left + leaves + right[::-1]
	
 
#time: o(n)
#memory: o(n)

Visual

Review 1
Just be mindful of the edge cases. Don’t add the root or leaf nodes in the left and right boundary traversal.

review