Link: https://leetcode.com/problems/combination-sum-ii/
Solution:
Topics: DFS, back tracking
Intuition
This is clearly a DFS backtracking problem, but I think its very tricky to come up with an efficient solution that will pass all the test cases. Initially, I interpreted this as a subsequence problem…more specifically, find all the subsequences that sum to target. This is not unreasonable, but treating this as a subsequence problem does not disallow duplicates in the final result because candidates are not distinct.
For example:
target = 6
[1,2,3,1,2,3]
^ ^ ^ sum([1,2,3]) = 6
[1,2,3,1,2,3]
^ ^ ^ sum([1,2,3]) = 6
As we can see, even though both [1,2,3] have distinct indices, if we treat this strictly as a subsequence problem, we would be adding [1,2,3] to the result twice. Not the end of the world, but then we would have to use a cache and keep the result in a set.
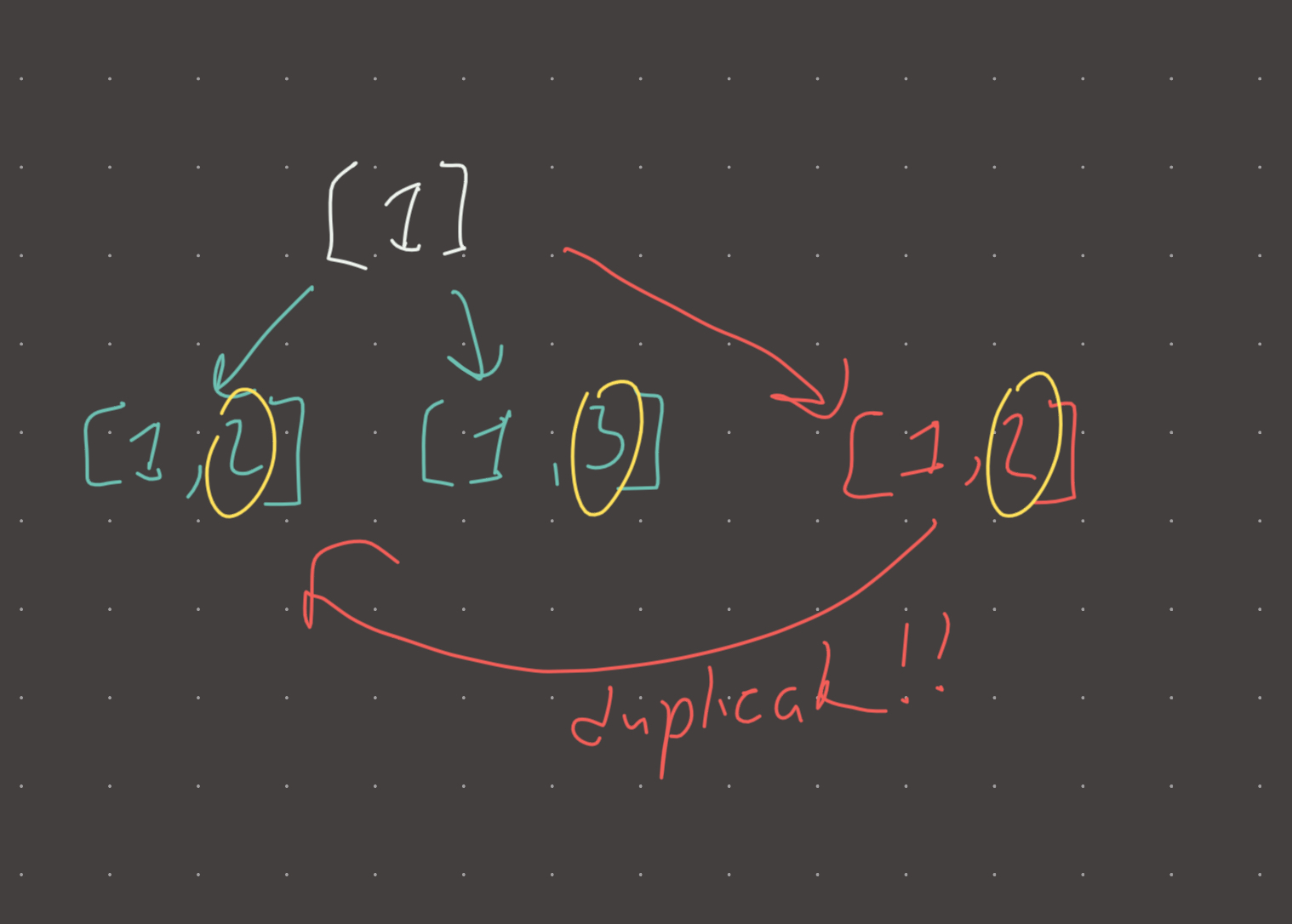
The optimal solution is to generate all the unique combinations outright. How can this be done? Basically, we must disallow duplicates in the same position in a common path.
For example:
candidates = [1,2,3,4,4], target = 10
current_path = [1,2,3]
If the current path is [1,2,3], we must ensure that NO DUPLICATE values can be added into the next position of the path.
So if the path is [1,2,3], we have two choices. Either to add the 4 at index 3 or the 4 at index 4.
If we add both 4's then we have duplicates:
[[1,2,3,4],[1,2,3,4]]
^ ^
So, the idea here is to keep moving the index, and only take disctinct values at each position.
Note that this does not prevent duplicate values in the result, this only prevents duplitate values in the same POSITION of the result.
For example [2,4,4] is fine becase there are two fours and they occur in different positions in the path.
Or in other tree terms, if we imagine path as the parent, then path can only have unique children.
Also, we must sort candidates in order to move the pointers in a way that prevents duplicates.
Implementation
def comb_sum(candidates, target):
candidates.sort()
res = []
def dfs(i, total, path):
if total > target:
return
if total == target:
res.append(path)
return
if i == len(candidates):
return
for j in range(i, len(candidates)):
if j > i and candidates[j] == candidates[j-1]:
continue
dfs(j+1, total + candidates[j], path + tuple(candidates[j]))
dfs(0, 0, ())
return res
#time: o(2**n)
#memory: o(n)Mnemonic
A parent can not have duplicate children.
Visual
Review 1
Very nice problem! I did get there but it took some brain power! The above implementation is kind of bad and doesn’t actually implement backtracking.
The key insight is understanding that we cannot reuse the same number in same position! So we structure our recursion such that duplicates are not possible…or in other words, we process all possible children before changing the parent (topological order)! Children in this case will be any index that is greater than the current one.
def combo2(candidates, target):
candidates.sort()
res = []
path = []
def dfs(i, total):
if total == target:
res.append(tuple(path))
return
if total > target or i == len(candidates):
return
for j in range(i, len(candidates)):
if j != i and candidates[j] == candidates[j-1]:
continue
path.append(candidates[j])
dfs(j+1, total + candidates[j])
path.pop()
dfs(0, 0)
return resReview 2
Solved it without much issue.