Constrained subsequence sum

Link: https://leetcode.com/problems/constrained-subsequence-sum/

Solution:

DSA: heap

Intuition
This seems like a take/skip DP pattern and while technically this works and the code is concise, it results in TLE because there exists a greedy solution using a max heap. I still don’t understand the intuition behind how to come up with this solution but the solution does make sense.

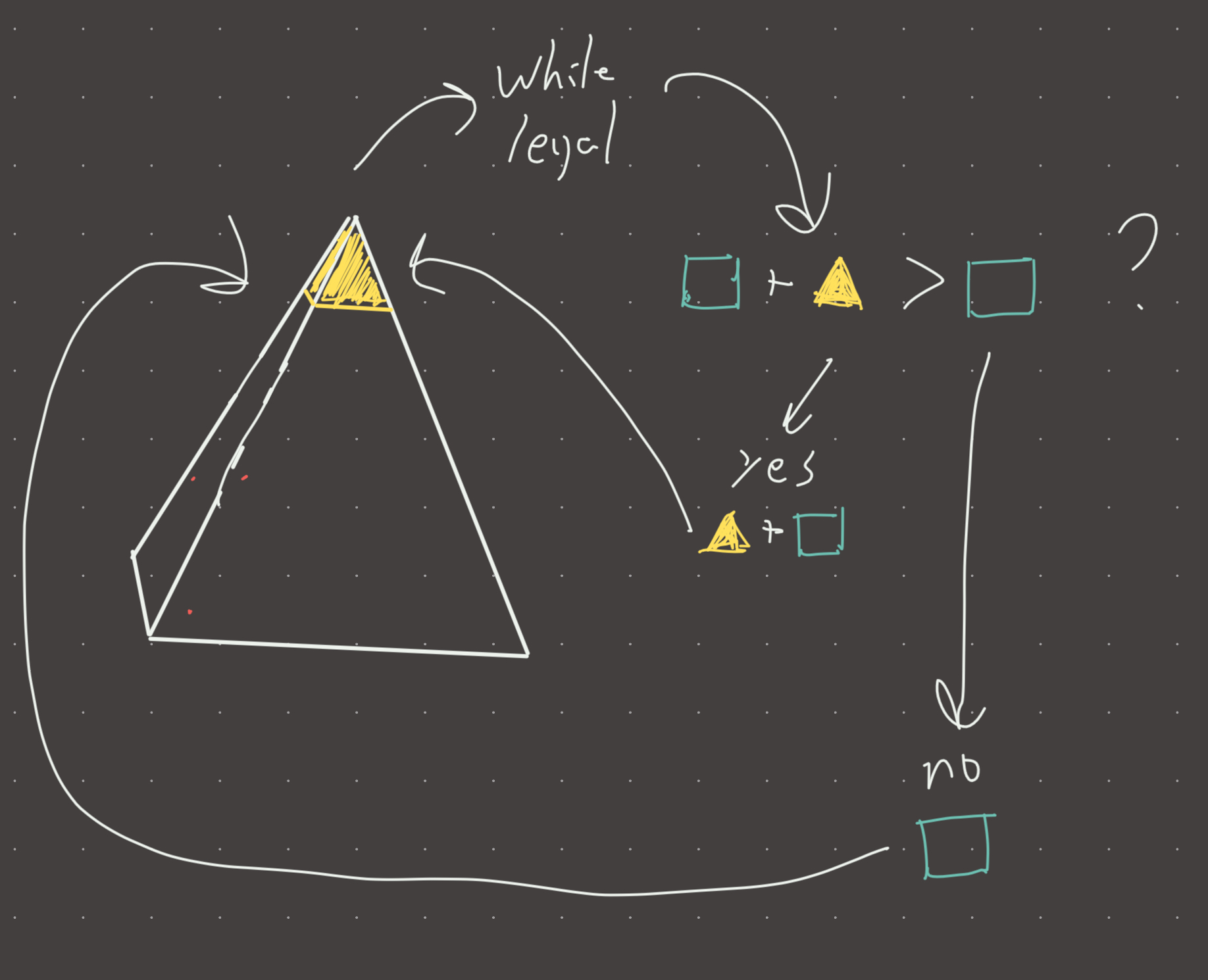
The key seems to be knowing that this is a variation on kadanes greedy algorithm. The idea is to keep a sliding window max_heap. Sliding window in the sense that while the top of the heap is outside the range that we can take from, we pop those elements and no longer consider them.

So as long as we maintain the heap such that its always ‘legal’ to take from the top, we can chose whether or not to take. Why do we have to choose? Because the top of the max_heap may be the highest we have seen so far, but if all we have seen are negative integers, it would be optimal not to take from the top if we see a higher negative or a positive (a negative plus any number is always smaller).

In the case that the max_heap[0] + nums[i] > nums[i], we would add nums[i] + max_heap[0] back into the heap with the current index. This represents a kind of reservoir that we deposit into and it conceptually represents the subsequence (factually its the subsequence sum). Otherwise, we just add (nums[i], i) back into the heap. Take the max.

The solution is difficult to come up with in part because the DP solution is the first thing that comes to mind. The code is pretty straight forward.

Implementation

#default python heap is MIN, so reverse the sign for a max_heap
def max_subseq(nums, k):
	res = nums[0]
	max_heap = [-(nums[0], 0)]
	
	for i in range(1, len(nums)):
		while i - max_heap[0][1] > k:
			heappop(max_heap)
		current = nums[i]
		if current + (-max_heap[0][0]) > current:
			current += -max_heap[0][0]
		heappush(max_heap, (-current, i))
		res = max(res, current)
	return res
 

Visual

Review 1
This is a very tricky problem. I fell into the DP trap for a second time here. To be honest, I have never seen a heap being used in this way, and the intuition is completely alien to me. That being said, the solution does make sense.

Basically, we are applying kadanes at every possible index but the current sum is not the running sum, rather it is the sum at the top of the heap. But first we “clean” the heap from subsequence sums that end at an index that we cannot select.

Essentially we maintain a heap of “running sums” (so to speak) and we constrain them by popping off the ones that cannot be selected. This is essentially kadanes, but we take our sum from the top of the heap (if it is inside the constraint)

review
hard
insane