Count nodes with the highest score

Link: https://leetcode.com/problems/count-nodes-with-the-highest-score/

Solution:

Topics: DFS, tree

Intuition
I really enjoyed this tree problem. I pretty much instantly knew how to solve it, but I spent a bit of time thinking about the optimal implementation from a memory standpoint.

The key idea here is that there can be at most only 3 components to consider:

1. The number of nodes in the left subtree
2. The number of nodes in the right subtree
3. The number of nodes connected to the parent (above)

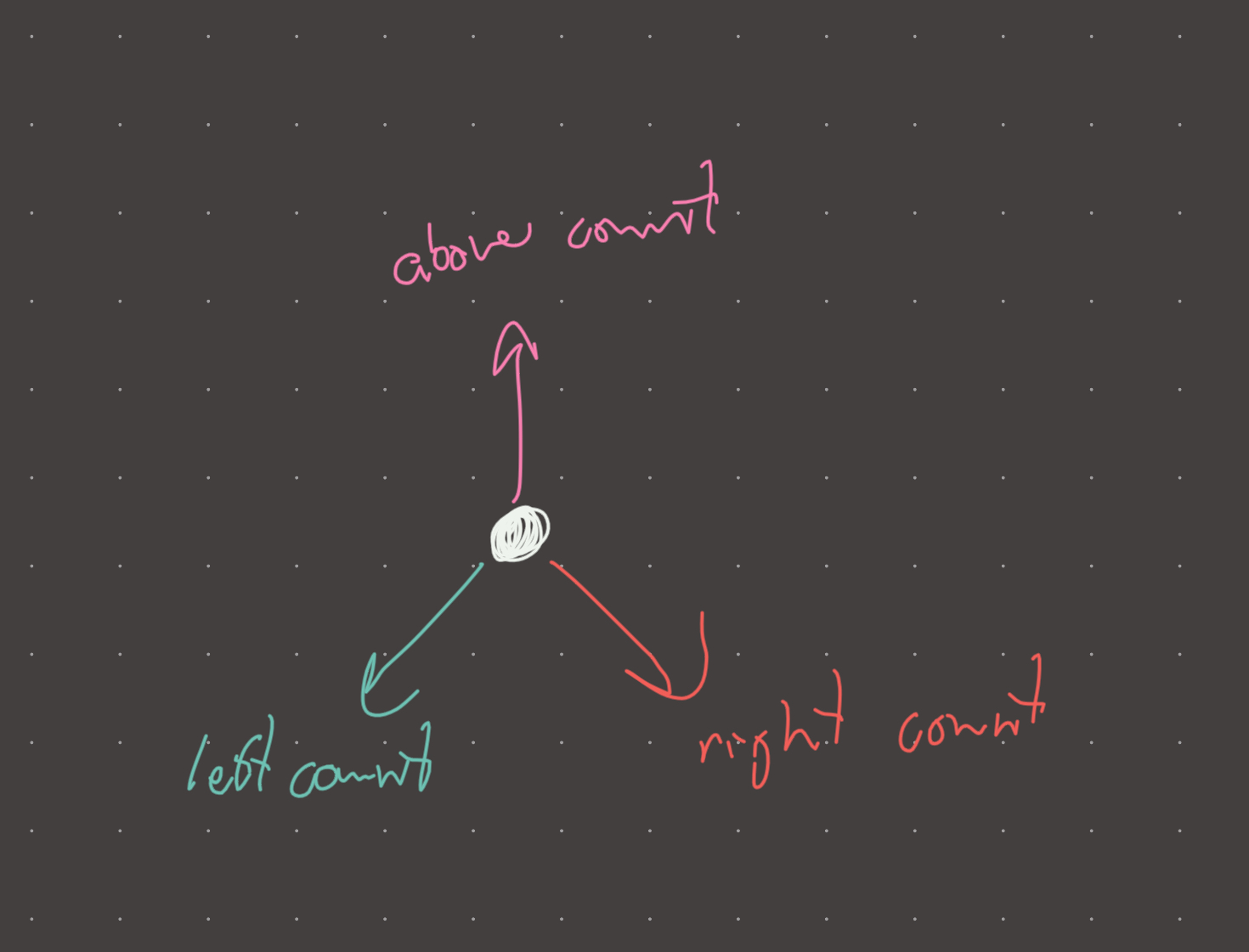
Number 1 and 2 are simple…we can just propagate a count from the leaves to the root, however #3 requires a little trick! The number of nodes in the “above” component will always be the total number of nodes subtracted by the number of nodes in the left component and the number of nodes in the right component…and -1 to subtract the current node!

above_count = n - left_count - right_count - 1

Basically, we can solve this recursively just as if we were solving for number of nodes in each subtree, but with some extra arithmetic to compute the score from the total.

There is one notable edge case. The root has no “above” component, so the derived formula will simplify to 0! This is problematic because the score is a product, so we must handle the root as a special case.

Also, the problem statement is (strangely) asking for the total number of nodes with the max score, so we need to store all scores for all nodes in our traversal, and then perform a frequency analysis.

Implementation

def count_nodes_score(parents):
	total_nodes = len(parents)
	adj = [[] for _ in range(total_nodes)]
	for child, parent in enumerate(parents):
		if parent == -1:
			continue
		adj[parent].append(child)
 
	scores = {}
	def dfs(node):
		if len(adj[node]) == 0:
			scores[node] = total_nodes - 1
			return 1
		children = 0
		score = 1
		for child in adj[node]:
			count = dfs(child)
			children += count
			score *= count
		score *= total_nodes - children - 1 if node != 0 else 1
		scores[node] = score
		return children + 1
	dfs(0)
 
	res = 0
	max_score = max(scores.values())
	for score in scores.values():
		if score == max_score:
			res += 1
	return res
			
#time: o(n)
#memory: o(n)

Review 1
Cool problem, super annoying implementation! Also, you don’t need scores hash map…some simple max logic and max_score, count variables would suffice.

review