Link: https://leetcode.com/problems/distribute-candies-among-children-i/
Solution:
Topics: permutation
Intuition
This problem seems more tricky than it really is, but the key is to look at the constraints. There can never be more than 3 children, and the limit of candies for each child can never be more than 50.
So with this information, we can compute that there are no more than 50^3 possible triplets. Thats not a whole lot, so pure brute force actually works here. Only a subset of these triplets can be valid since we must distribute ALL candies, therefore the sum of the triplet must equal the number of candies (n).
We can actually make a simple optimization to bring the complexity down from n^3 to n^2 by computing the last element in the triplet directly. If the sum of the triplet must by equal to n, then k = n - (i + j). If k is greater than limit or smaller than 0, the triplet is invalid.
My first solution to this problem was an optimized DFS, but the nested for loop here is way more elegant and memory efficient.
Implementation
def distribute_candies(n, limit):
ways = 0
for i in range(limit+1):
for j in range(limit+1):
k = n - (i + j)
if k >= 0 and k <= limit:
ways += 1
return ways
#time: o(n**2)
#memory: o(1)Visual
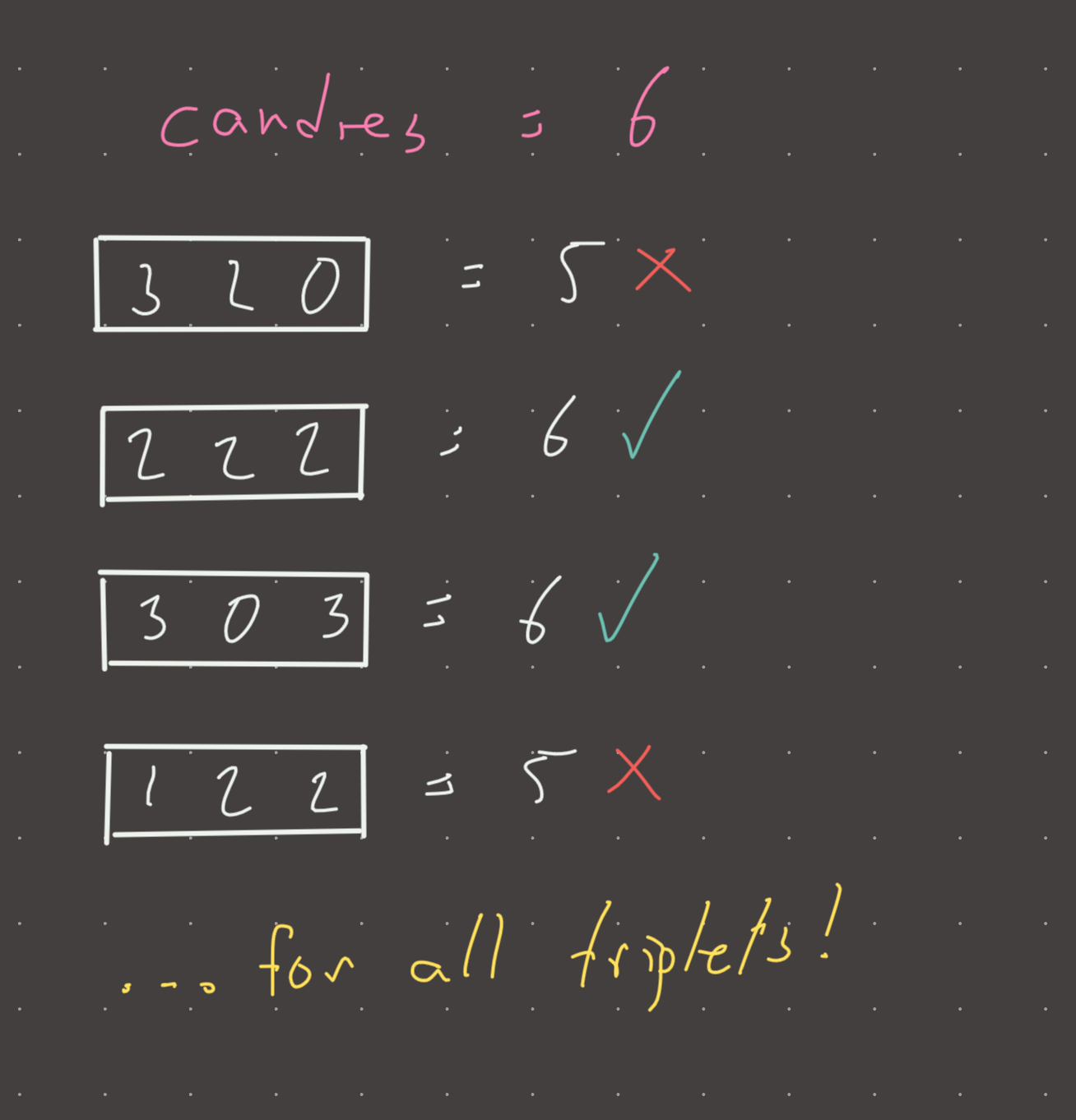
Mnemonic:
Triplets of children in queue entering candy store
Review 1
This is a great problem! I initially found the DFS solution but upon seeing the poor performance of the submission, I started to look for a better solution. I’m quite pleased that I managed to find the iterative solution because I have not seen many problems of this type and non-recursive permutation solutions are less intuitive to me at this point.
The key insight is that we have a hard constraint on the amount of candies given to the third child. If we give x candies to child 1 and y candies to child 2, then we must give n-(x+y) candies to child 3 in order to stay at exactly n candies given out!
What this means is that we can bring this problem down to n*n time complexity since the third number can be mathematically derived!
If the third number is greater than -1 and is under or at the limit, we can increment our result. But will this count all the possible permutations? This depends on how we set up our iteration.
if we allow i and j to iterate over the entire range 0-limit then inevitable we will get permutations of i, j, and since k if fixed to complete n, this accounts for all the permutations. Why? Because if the range is 0-1 and the iteration is unconstrained, we will get the following values for i, j:
i, j
----
0, 0
0, 1 -->
1, 0 --> same numbers reached, different permutation, and k is fixed
1, 1
I’m giving this one a hard label, which may seem comical for an easy problem but this solution is unnatural to me so I’d like to keep this one in the hard filter.