Erect the fence

Link: https://leetcode.com/problems/erect-the-fence/

Solution:

DSA: convex hull, monotone chain, math, stack

Intuition
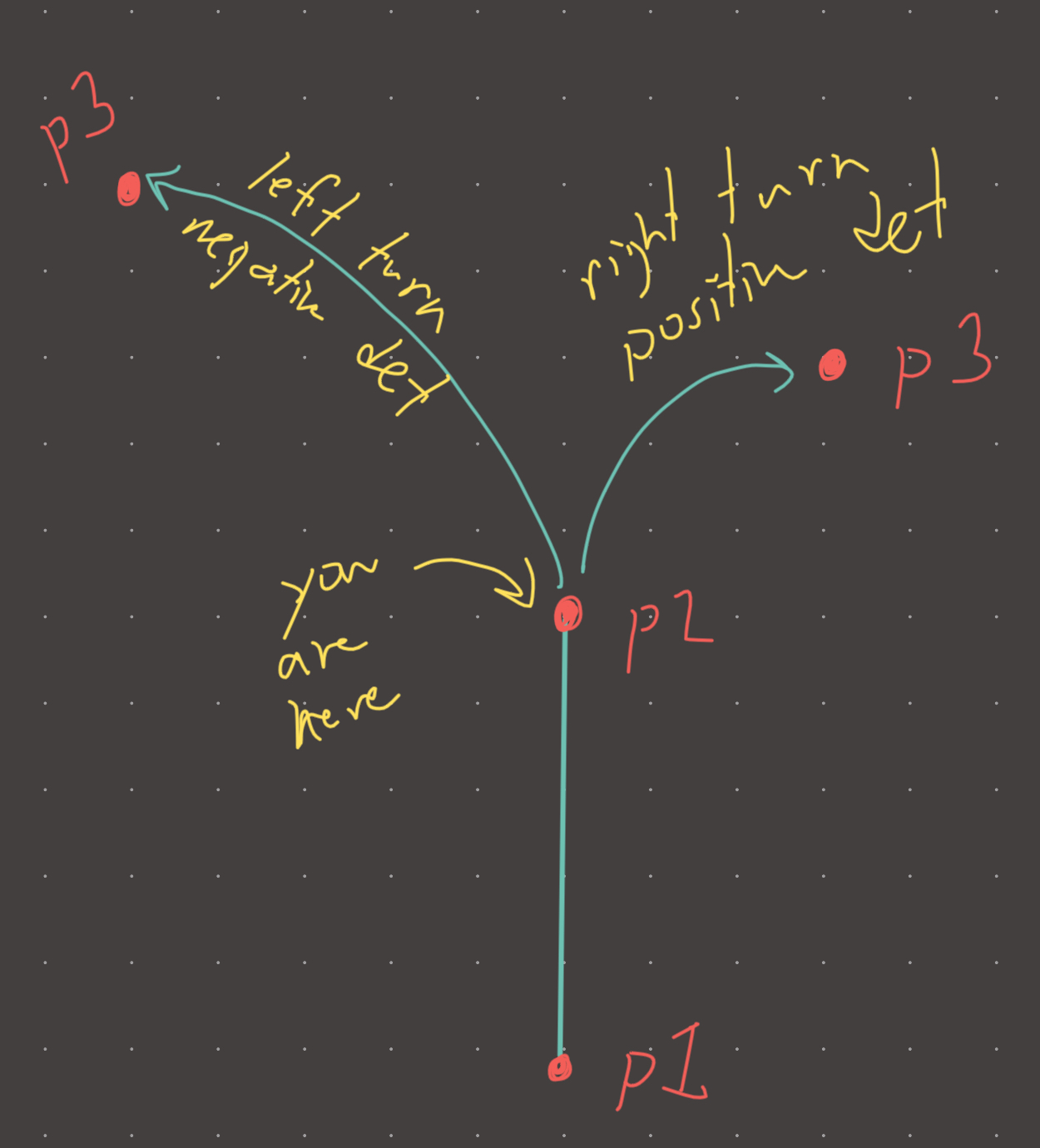
The core intuition is that the determinant of 3 points is positive if the 3rd point creates a left turn, and negative if it creates a right turn.

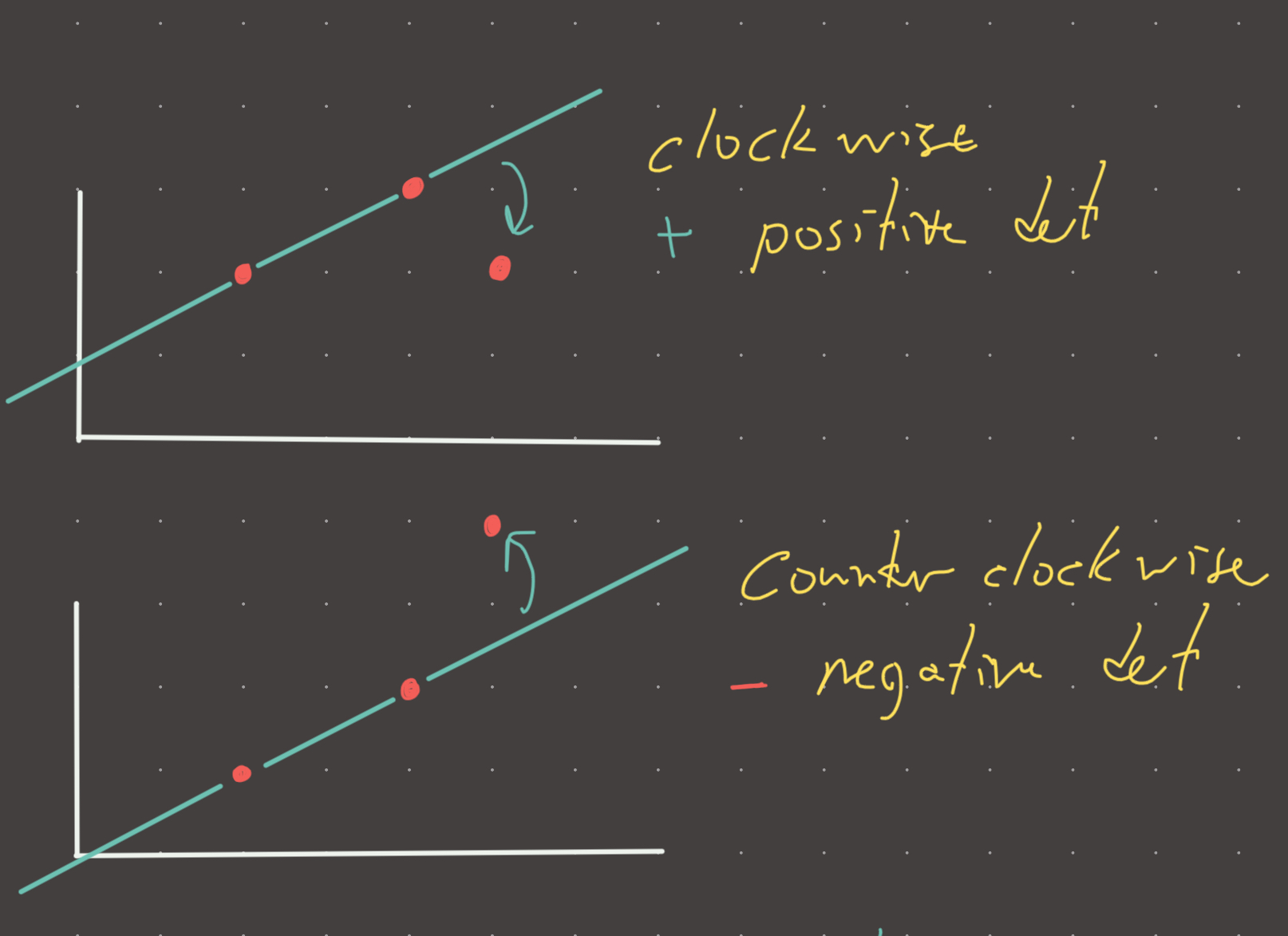
We can use this property to our advantage if we split up the fence into a top and a bottom! For the top, we want each point to be turning right, and for the bottom, each point to be turning left. This can be enforced mathematically by taking the determinant of 3 points.

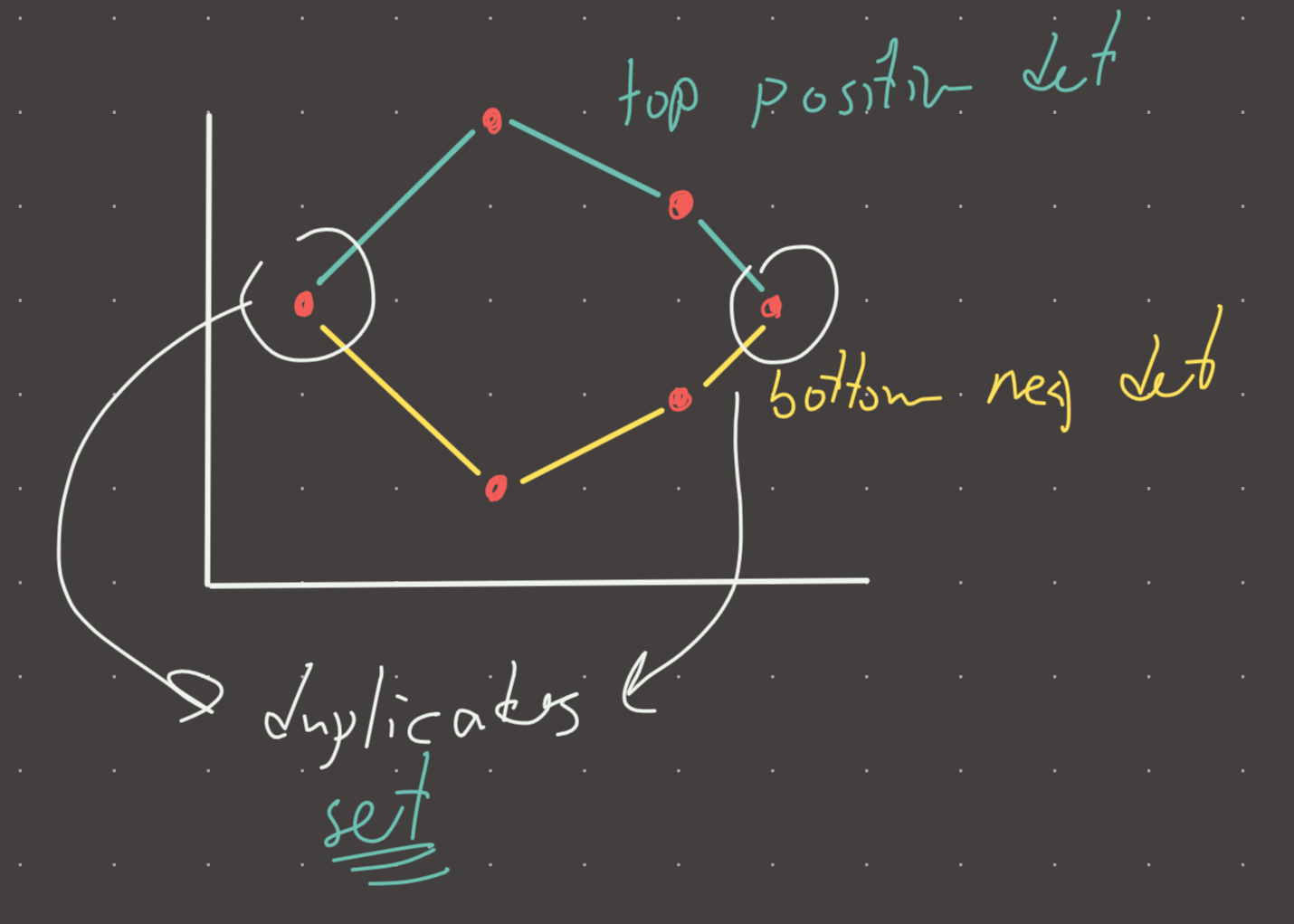
The idea is to sort the points from left to right and keep a stack for both lower and upper segments. These stacks will be monotonic in the sense that the top 3 points on the stack MUST have a positive determinant or negative determinant for upper and lower stack respectively.

At the end of the left to right point traversal, the upper and lower stacks will contain all the vertices of the fence. Combine them in a set to eliminate duplicates (see image above)

Implementation

def fence(trees):
	def det(p1, p2, p3):
		x1, y1 = p1
		x2, y2 = p2
		x3, y3 = p3
		determinant = (x2-x1)*(y3-y1) - (x3-x1)*(y2-y1)
		return determinant
		
	trees.sort()
	upper = []
	lower = []
	for tree in trees:
		#remove points that cause negative determinant
		#only positive is permitted for upper hull
		while len(upper) >= 2 and det(upper[-2], upper[-1], tree) < 0: 
			upper.pop()
			
		#remove points that cause positive determinant
		#only negative is permitted for lower hull
		while len(lower) >= 2 and det(lower[-2], lower[-1], tree) > 0:
			lower.pop()
		upper.append(tree)
		lower.append(tree)
		
	return list(set(lower+upper)) #there will be duplicates, see image above

Visual

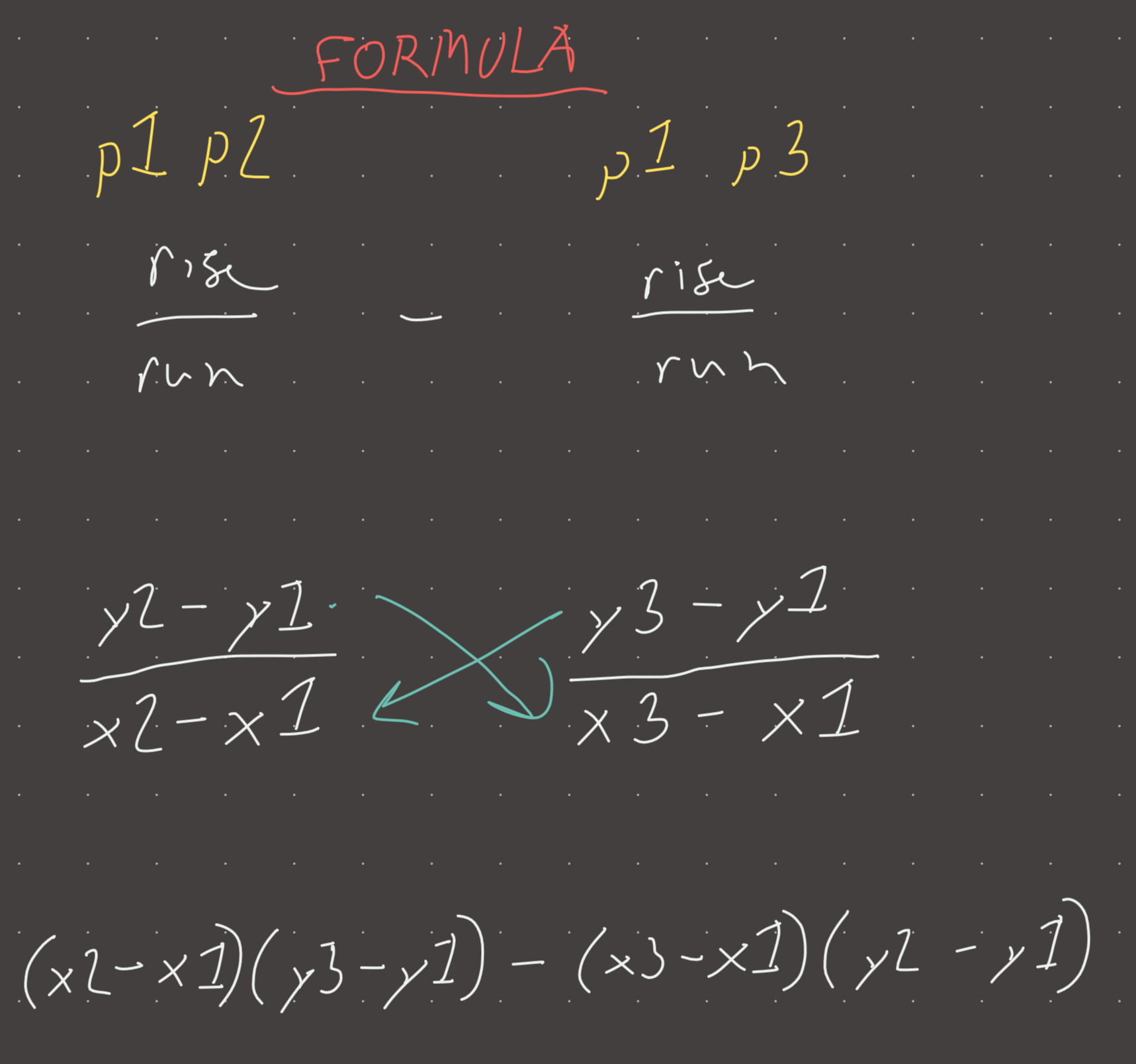
Review 1
The above solution is kind of absurd and unintuitive. Monotone chain is waaaaaaay simpler and intuitively makes alot more sense.

The key idea is to solve in 2 passes. The lower hull, and then the upper hull. Basically, we sort by X and then keep a monotonically increasing stack based on the slope with the current tree and the top of the stack. Do the same in reverse and add every tree in both stacks to a set…this is the result.

Note: when we compute slope with the formula (y-y2)/(x-x2), division by 0 is possible so give these cases a slope of inf as these trees are right on top of each-other and draw a straight line up the graph. In some cases these trees will draw the left or right boundary so they must be considered.

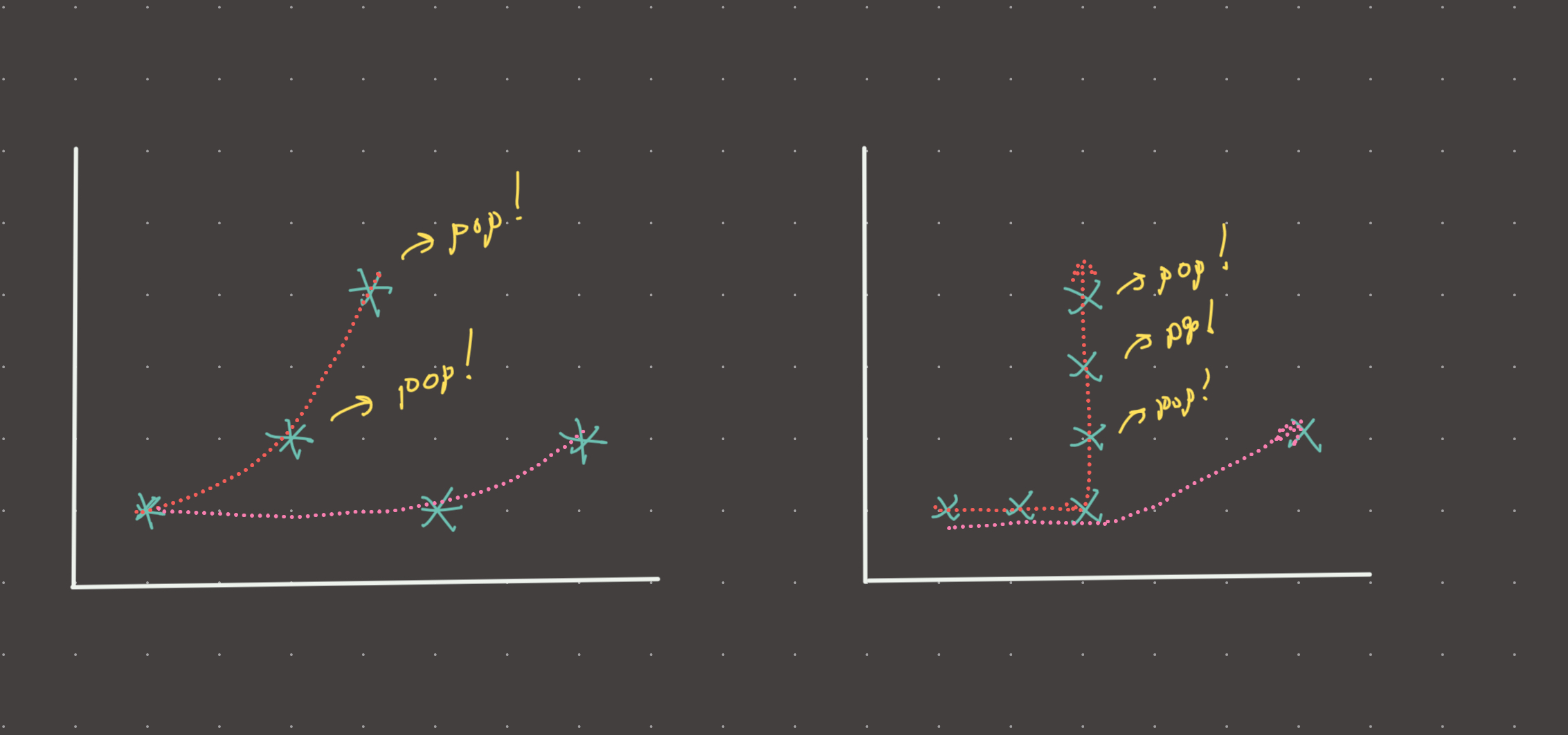
review
hard
niche