Link: https://leetcode.com/problems/evaluate-division/
Solution:
Topics: graph, DFS, BFS, union find
Intuition
This is a great but very tricky graph problem. I was quite pleased that I solved this one on my first attempt. The trickiest part of this problem is realizing that we need to use a graph. Essentially we must build a graph where the edges represent the value we get from dividing two nodes. From there, its simply a matter of finding a path between A, B in a query and the value is the product of all edges in the path.
I realized that this was a graph problem when it occurred to me that for an equation a/b = value1, a can be written as a = b*value1, and for equation b/c = value2, can be written as b = c*value2…therefore for the query [a, c], can be written as a = c*value2*value1 or simply as a/c = value2*value1. Basically, if there exists a path between a and c, there is an answer.
The last insight was remembering that if a/b = x, b/a = 1/x. So we have a kind of undirected graph, but going backwards would reciprocate the weight of the edge. This can also be interpreted as a directed graph with two edges between nodes. I prefer the pseudo-undirected interpretation because it emphasizes that cycles will be possible.
There is also a union find solution but I wont get into it now.
Implementation
def eval_div(equations, values, queries):
adj = {}
for (a, b), val in zip(equations, values):
if a not in adj:
adj[a] = []
if b not in adj:
adj[b] = []
adj[a].append((b, val))
adj[b].append((a, 1/val))
def bfs(start, end):
if start not in adj or end not in adj:
return -1.0
visited = set()
queue = deque([(start, 1)])
while queue:
node, val = queue.popleft()
if node in visited:
continue
if node == end:
return val
visited.add(node)
for neighbor, multiply in adj[node]:
queue.append((neighbor, val*multiply))
return -1.0
res = []
for a, b in queries:
res.append(bfs(a, b))
return res
#time: o(nm) n=len(queries), m=nodes in graph
#memory: o(m)Visual
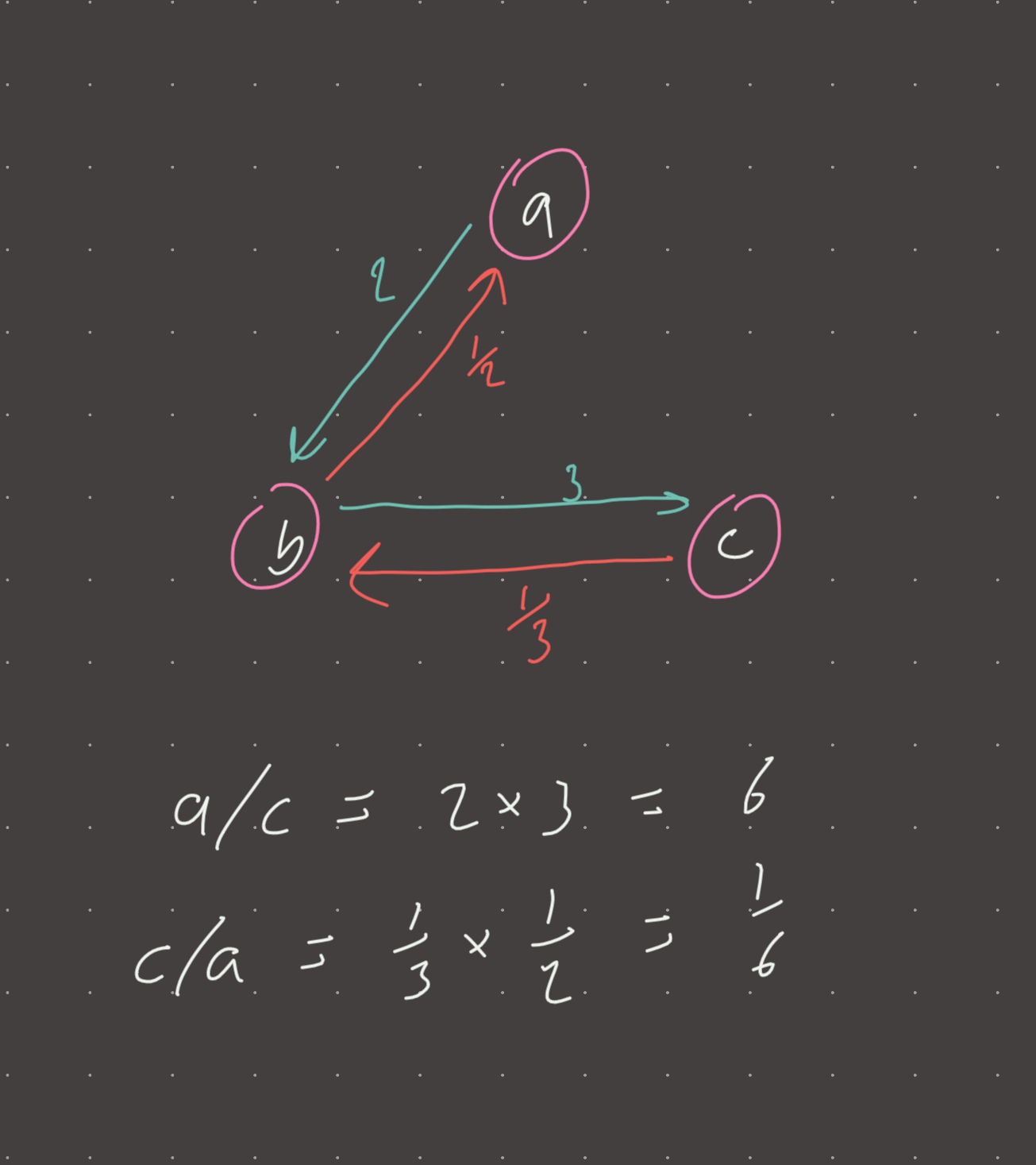
Review 1
Tricky, but I crushed this one on first try again.