Link: https://leetcode.com/problems/find-median-from-data-stream/
Solution:
Topics: heap
Intuition
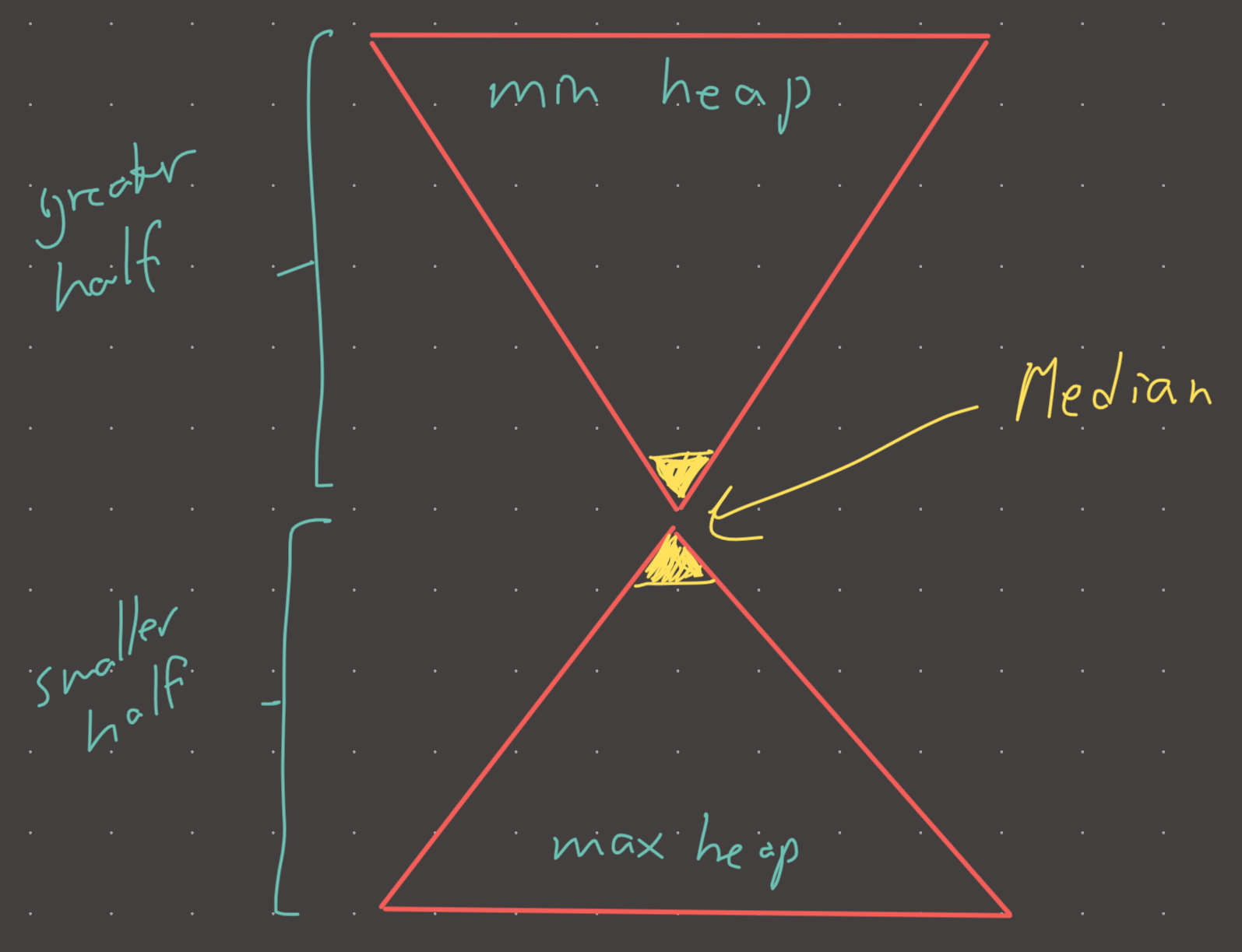
The key to this problem is keeping the smaller half of the data in a max heap and the greater half of the data in a min heap. If this can be accomplished, then the top of the each heap will converge exactly to the median. Why?
consider the following sorted list
nums = [1,2,3,4,5,6]
if we split nums in half we get the following:
nums1 = [1,2,3]
nums2 = [4,5,6]
the median consists of 3 and 4...now think about the their positions. 3 is the last element in the smaller partition, and 4 is the first element in the greater partition. How can we always know where these elements are? Heaps!
If we store nums1 in a max_heap, then max_heap[0] would be 3. Similarly, if we store nums2 in a min_heap, then min_heap[0] would be 4. If len(nums1) + len(nums2) is odd, the median is the top of the bigger heap.
If the heaps get out of balance, its necesary to rebalance them. Why?
Suppose we didnt know which element in nums was coming next.
current | min_heap | max_heap
-----------------------------
1 | [1] | [] #min_heap is longer so 1 is the median...correct
2 | [1, 2] | [] #min_heap is still longer but 1 is not the median!
balance | [2] | [1] #balance the heaps, median is 1.5...correct.
when len(heap1) - len(heap2) == 2, pop from the longer one and push the element to the shorter one!
Implementation
class median_finder:
def __init__(self):
self.min_heap = []
self.max_heap = []
def add_num(self, num):
if len(self.min_heap) == 0:
heappush(self.min_heap, num)
else:
if num < self.min_heap[0]:
heappush(self.max_heap, -num)
else:
heapush(self.min_heap, num)
if len(self.min_heap) - len(self.max_heap) == 2:
heappush(self.max_heap, -heappop(self.min_heap))
if len(self.max_heap) - len(self.min_heap) == 2:
heappush(self.min_heap, -heappop(self.max_heap))
def find_median(self):
n = len(self.min_heap) + len(self.max_heap)
if n % 2 == 0:
return (self.min_heap[0] + self.max_heap[0])/2
else:
if len(self.min_heap) > len(self.max_heap):
return min_heap[0]
else:
return -max_heap[0]
#time: o(nlogn) ...for n calls
#memory: o(n)Visual
Review 1
Straight forward, but remember to push the first num to the max_heap (left partition) if comparing against min_heap. This prevents some edge cases.