Link: https://leetcode.com/problems/find-the-closest-palindrome/
Solution:
Topics: binary search
Intuition
This is a pretty tough problem. There are two approaches, but the binary search approach is way more intuitive to me.
The idea is to search for the next palindrome and the previous palindrome, and then return the closer (or smaller) of the two. But how do we turn this into a binary search problem?
We know that the result will be in the range between 0 - 10^18, but we can’t really use these numbers directly because there is no guarantee, in fact its highly unlikely, that where we land in the binary search will be a palindrome. So how do we get around this?
Its very simple. We can convert the number into its smallest palindrome by mirroring the left half. This also gives us our sorted property because if the resulting palindrome is greater or smaller than int(n), it is guaranteed that all numbers to the right or left respectively will also be greater or smaller.
For example:
l = 0
r = 100
mid = 50
palin = 55
It can be shown that all numbers to the right of 50 can never yeild smaller palindromes than 55.
Effectively, this means we are searching through a range of palindromes with many duplicates:
mid = ... 48, 49, 50, 51, 52, 53 ...
palin = ... 44, 44, 55, 55, 55, 55 ... # converted to palin
The duplicates don't matter as the list is still sorted and the complexity is logn.
The reason we mirror the left half is to ENSURE the sorted order.
Essentially, by converting every number to a palindrome in this way, we are generating all possible palindrones in a range, will many duplicates yes, but sorted.
So now that we have converted this problem into binary search, we need to look at the problem statement. We are asked to find the closest palindrome, which can either be greater than int(n) or smaller.
It should be clear that we can use two binary searches. One to find the smallest possible palindrome in the range num - 10^18 and one to find the largest possible palindrome in the range 0 - num. Simply return the closer or smaller in the case of a tie.
Implementation
def closest_palin(n):
def convert(num):
s = list(str(num))
l = 0
r = len(s) - 1
while l < r:
s[r] = s[l]
l += 1
r -= 1
return int(''.join(s))
def bs_smaller(num):
res = float('inf')
l = 0
r = num
while l <= r:
mid = (l + r) // 2
palin = convert(mid)
if palin < num:
res = palin
l = mid + 1
else:
r = mid - 1
return res
def bs_greater(num):
res = float('inf')
l = num
r = 10**18
while l <= r:
mid = (l + r) // 2
palin = convert(mid)
if palin > num:
res = palin
r = mid - 1
else:
l = mid + 1
return res
smaller = bs_smaller(int(n))
greater = bs_greater(int(n))
return str(min(smaller, greater, key=lambda x: (abs(x-int(n)), x)))
#time: nlog(int(n)) + nlogm
#memory: o(n) because of conversionVisual
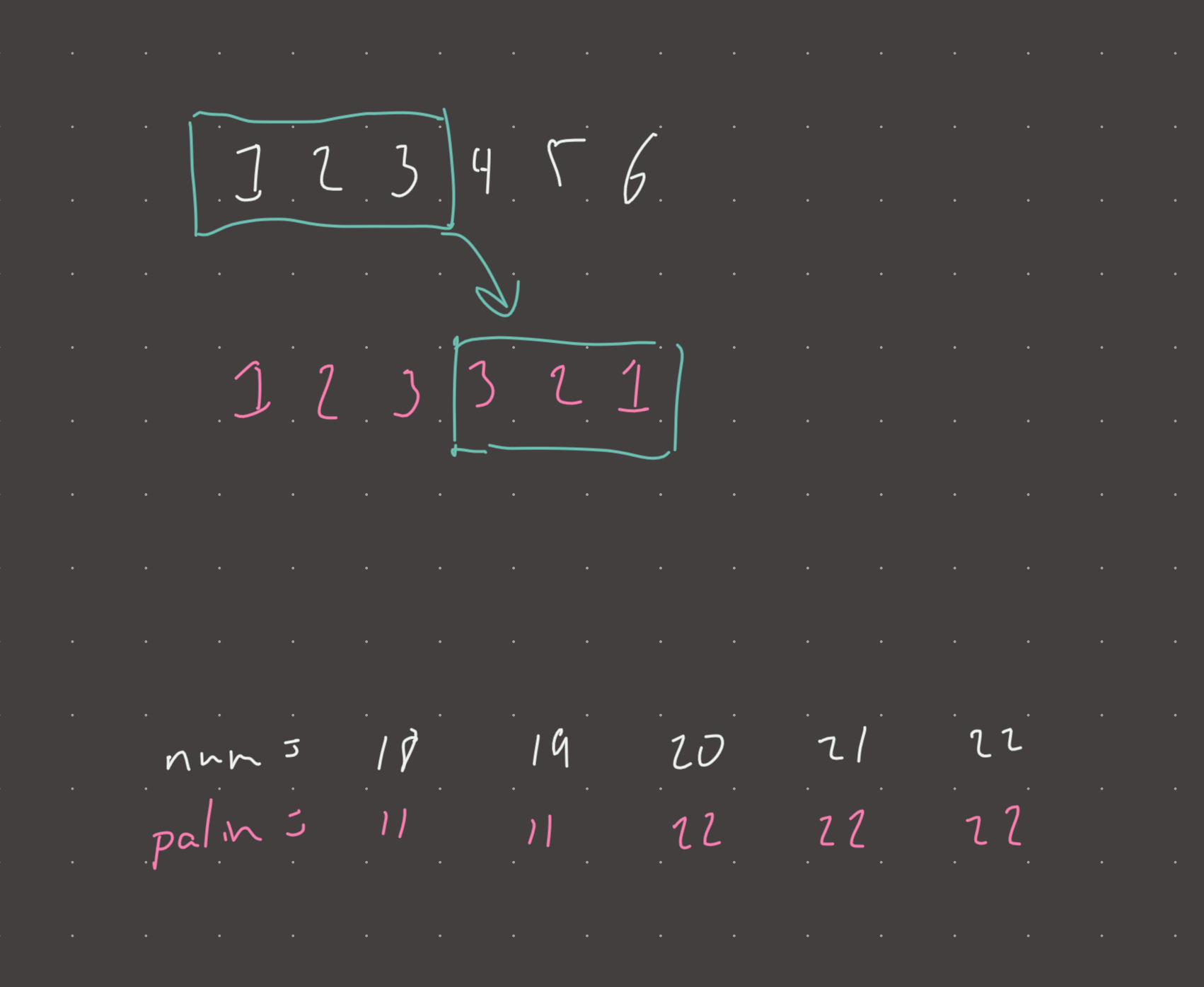
Review 1
Insane problem! I will admit, even the second time around I did not make the connection to binary search. I did understand that the smallest change to make a number a palindrome would be mirroring the left half, but it was not clear to my why we wouldn’t just do this for n in o(1) time. Well, you can almost do that, but the constraints prevent it. Why?
Well, what if n was already a palindrome? Mirroring it would just return itself, which is not permitted.
Also, if n == 999, we have two possible palindromes: 989, 1001. This is all pretty reasonable, but how do we implement this programatically? Binary search!
We can search in the range 0-n for the largest palindrome and search n-(10**18) for the smallest palindrome!
But how do we search through those ranges while ensuring the numbers are all palindromes? Here is the neat part: you don’t. This is some binary search witchcraft, yet it’s so simple. We simply convert the number to it’s closest palindrome by mirroring the left partition. This way, yes we get many duplicate palindromes, but it doesn’t matter because it’s binary search!
original: ...21, 22, 23, 24, 25...
converted: ...22, 22, 22, 22, 22...