Link: https://leetcode.com/problems/furthest-building-you-can-reach/
Solution:
Intuition
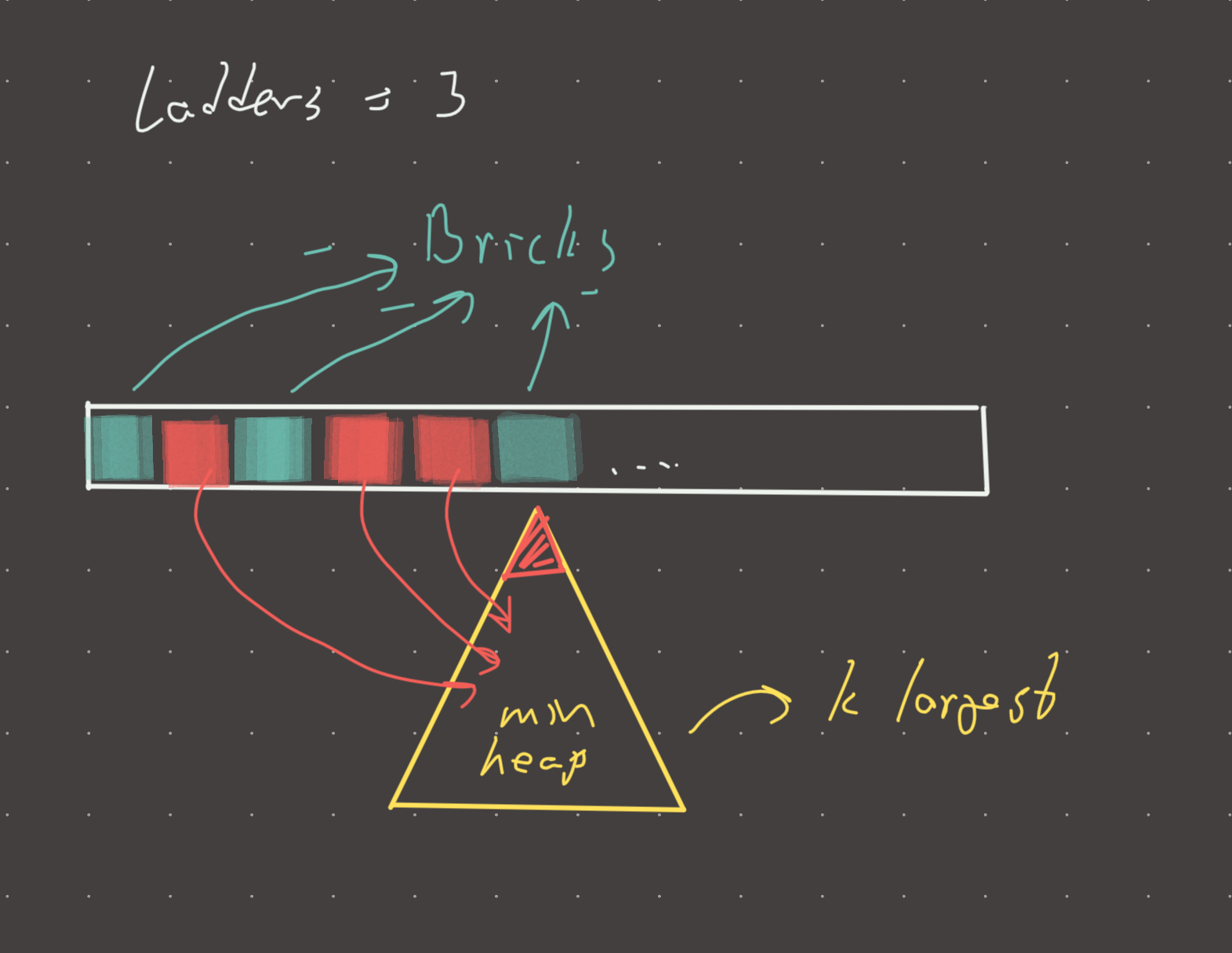
This is a very nice heap problem. The idea is to keep the K largest deltas in a min_heap where K is equal to the number of ladders. I initially solved this with binary search but that approach is less optimal.
The intuition here is to only use ladders on the largest deltas seen so far! If the size of the heap exceeds K, we pop off the min_heap and subtract the popped delta from bricks. When bricks is smaller than zero, we can’t make the next jump.
This is a pretty cool application of heap because the optimal strategy is of course to use ladders on the largest deltas, and the heap allows us to keep the largest deltas seen at any moment. In a way, the strategy dynamic and self-adjusting because we can envision cases where getting to building X requires a different application of ladders (and in different order) than getting to building Y.
Implementation
def furthest_building(heights, ladders, bricks):
min_heap = []
for i in range(1, len(heights)):
delta = heights[i] - heights[i-1]
if delta <= 0:
continue
heappush(min_heap, delta)
if len(min_heap) > ladders:
bricks -= heappop(min_heap)
if bricks < 0:
return i - 1
return len(heights)-1
#time: o(nlogn)
#memory: o(n)Visual
Review 1
Again, I solved it very quickly with binary search but the pure heap solution evaded me! The heap solution is insanely clever so I don’t feel too bad! Maybe I would have gotten there if I spent more than 5 minutes on it.
Basically we keep a min_heap of all the positive differences (jumps that must use either bricks or a ladder). If the length of the heap is smaller than ladders, it means we don’t have to use even a single brick. If the length is greater than ladders, we pop off the heap and we decrement bricks by that difference!
The intuition is quite hard because the mind goes to using ladders greedily with a max_heap, but here we are doing the reverse! The min_heap creates a kind of implied greedy usage of ladders and we only use bricks when the heap exceeds the number of ladders!
This is basically the same as Kth largest element in an array! But in this case we are keeping our k is ladders! So we are guaranteed to have all the largest differences at any point in the heap!