Link: https://leetcode.com/problems/gas-station/
Solution:
Topics: greedy, sliding window, simulation
Intuition
This is a pretty tricky problem, but we can essentially simulate the outcome using a few key assumptions.
It is natural to simulate this problem with a gas tank. gas_tank += gas[i] - cost[i]
If gas_tank < 0 at the current index, we can’t move to the next station, so reset gas_tank to 0, and set potential_start to i+1.
The notable edge case is if the cost of the round trip exceeds the gas available…in which case its not possible to make the round trip. Return -1.
Implementation
def gas_station(cost, gas):
if sum(cost) > sum(gas): #handle edge case
return -1
gas_tank = 0
potential_start = 0
for i in range(len(gas)):
gas_tank += gas[i] - cost[i]
if gas_tank < 0:
gas_tank = 0
potential_start = i + 1
return potential_start
#time: o(n)
#memory: o(1)Mnemonic
Drive car to gas station until tank empty (negative), then walk to next station and get a new car to continue the journey.
Visual
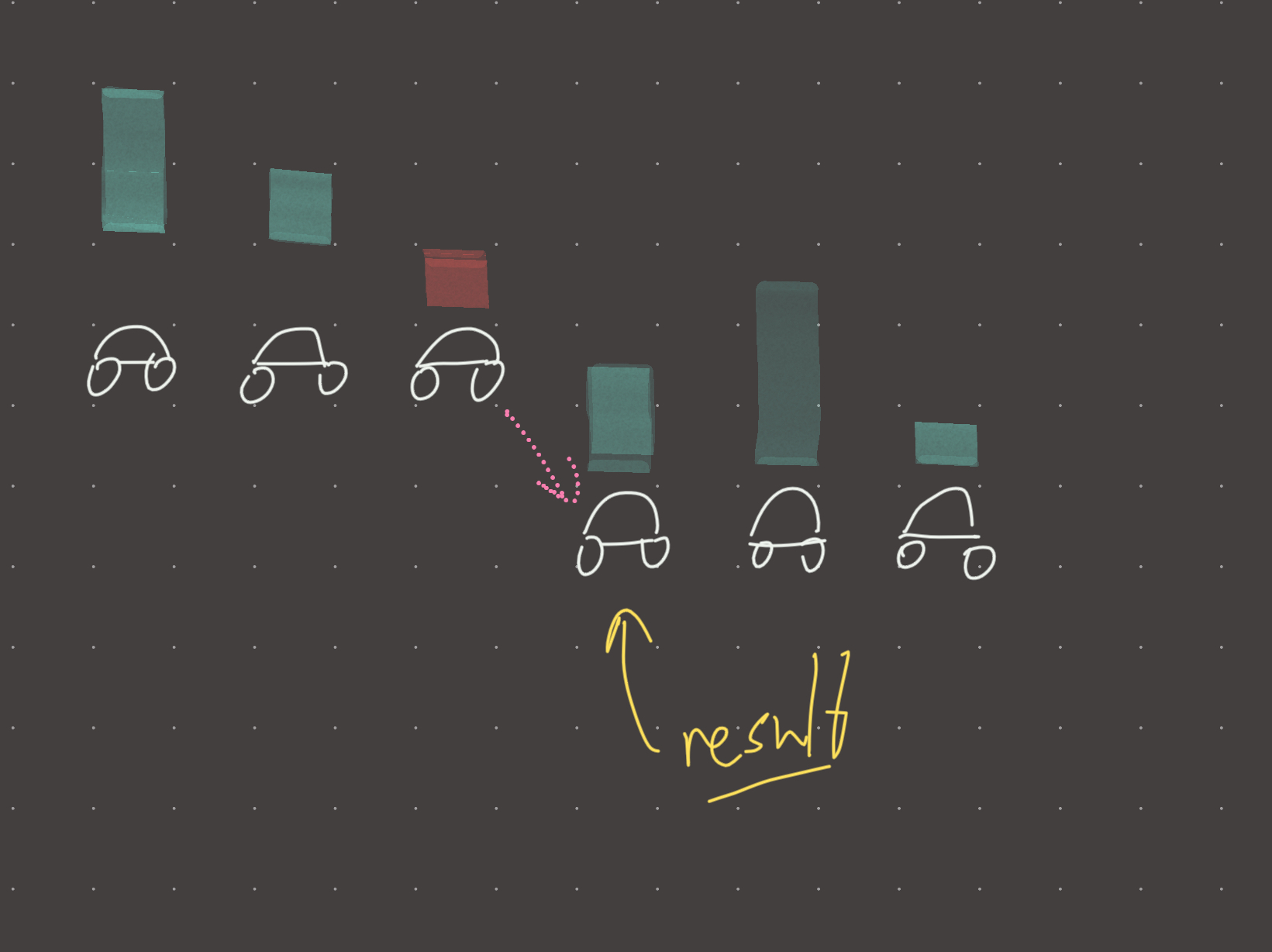
Review 1
Great little problem, and Im glad to have solved this one easily as I had tagged this as hard prior. Basically we need to understand two things.
- we can continue the journey
- we can restart the journey
We can continue the journey if our gas tank (after adding the gas and subtracting the cost) is greater or equal to 0. Otherwise, we are forced to restart the journey. This is not too different from a kadanes algorithm.
As far as the implementation goes, we can keep track of our starting point and if we wrap around back to it, we can return that index.
The implementation above is kind of tricky to understand but it leverages the fact that the only case -1 is a possible result is if the sum(cost) > sum(gas). This is the case because if that is true, you can never have enough gas to lap the circuit, if its not the case, then there will always be a starting point that allows for completion.
For example:
gas = [0, 0, 0, 0, 10]
cost = [2, 2, 2, 2, 2]
We can see that gas station 5 (and no other) gives us all the gas required to complete the circuit.
Also, sum(gas) must equal sum(cost)...otherwise there is more than one starting point (potentially), so there are multiple answers.
This approach is kind of unintuitive IMO, so I prefer iterating over len(gas)*2 and using modulus to normalize the index. If index % gas == start, we have completed the circuit and can return the start. This is not less efficient than the above solution because both sum(cost), sum(nums) are o(n) operations.
Implementation (wrap)
def gas_station(cost, gas):
gas_tank = 0
start = 0
for i in range(len(gas)*2):
index = i % len(gas)
if i > start and index == start:
return start
gas_tank += gas[index] - cost[index]
if gas_tank < 0:
gas_tank = 0
start = i + 1
return -1