Integer break

Link: https://leetcode.com/problems/integer-break/

Solution:

DSA: DP, math, shrink

Intuition (DP)
The intuition for the DP solution is pretty simple. We subtract 1-n recursively until n = 0 and return zero. Make sure to handle the edge case when n by itself is greater than any product of its sums. Why?

For example:

n = 1
#the only possible break is [0, 1] and the product is 0

n = 2
#the only possible break is [1, 1] and the product is 1

n = 3
#the best possible break is [2, 1] and the product is 2

Handle these edge cases manually otherwise the recursive function will return n...so for n < 4 return n-1

Implementation (DP)

def integer_break(n):
	if n < 4:
		return n-1
		
	@cache
	def dfs(n, product):
		if n == 0:
			return product
			
		max_prod = 1
		for i in range(1, n+1):
			max_prod = max(max_prod, dfs(n-i, product * i))
		return max_prod
 
	return dfs(n, 1)
		
 
#time: O(n**2)
#memory: O(n)

Intuition (math)
The second approach is a bit more interesting. Turns out that it can be mathematically proven that if we greedily multiply by 3, this will always result in the maximum product! If division by 3 has a remainder of 2, multiply by 2 at the end. If the division by 3 has a remainder of 1, then take away a single multiplication by 3 and multiply by 4 instead!

def integer_break(n):
	if n < 4:
		return n-1
 
	if n % 3 == 1:
		return 3**(n//3 - 1) * 4
	if n % 3 == 2:
		return 3**(n//3) * 2
	else:
		return 3**(n//3)
 
#time: O(logn) because exponentiation is usually logn
#memory: O(1)

Visual

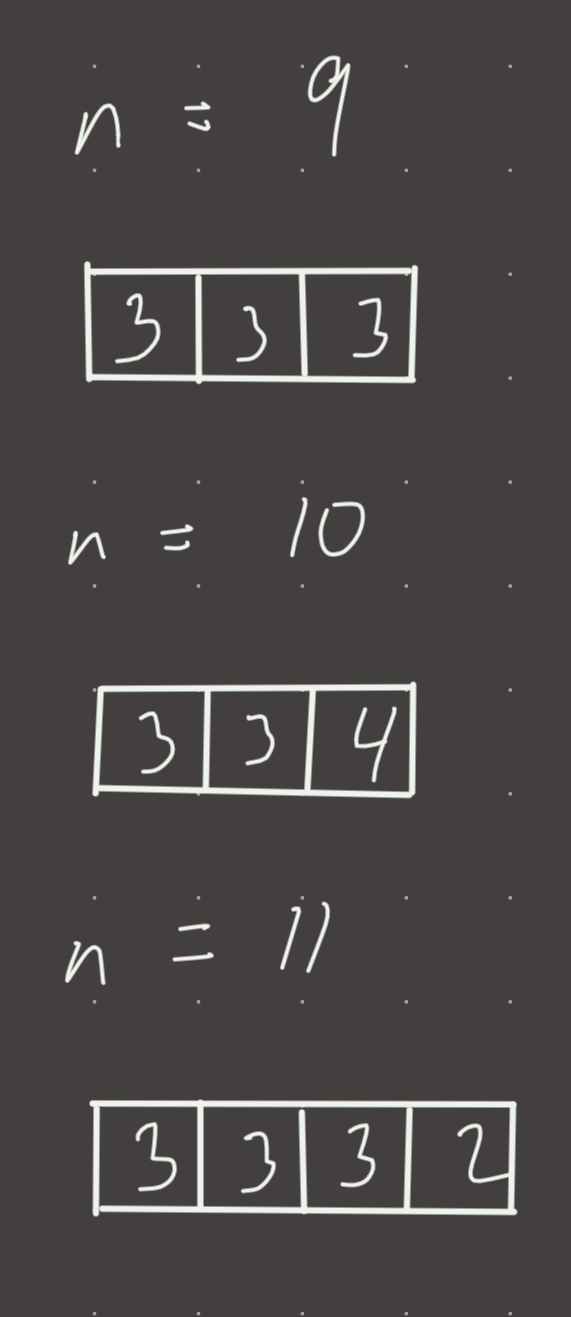
Review 1
I actually remembered that we can greedily take 3’s away from n for the max product. There are some edge cases though.

1. If the remainder of n % 3 == 1 then we take one 3 away and multiply by 4.
2. If n % 3 == 2 then take all the 3’s and multiply by 2.
3. if n % 3 == 0 take all 3’s.
4. if n < 4 return n-1

review