Knight dialer

Link: https://leetcode.com/problems/knight-dialer

Solution:

DSA: DP

Intuition
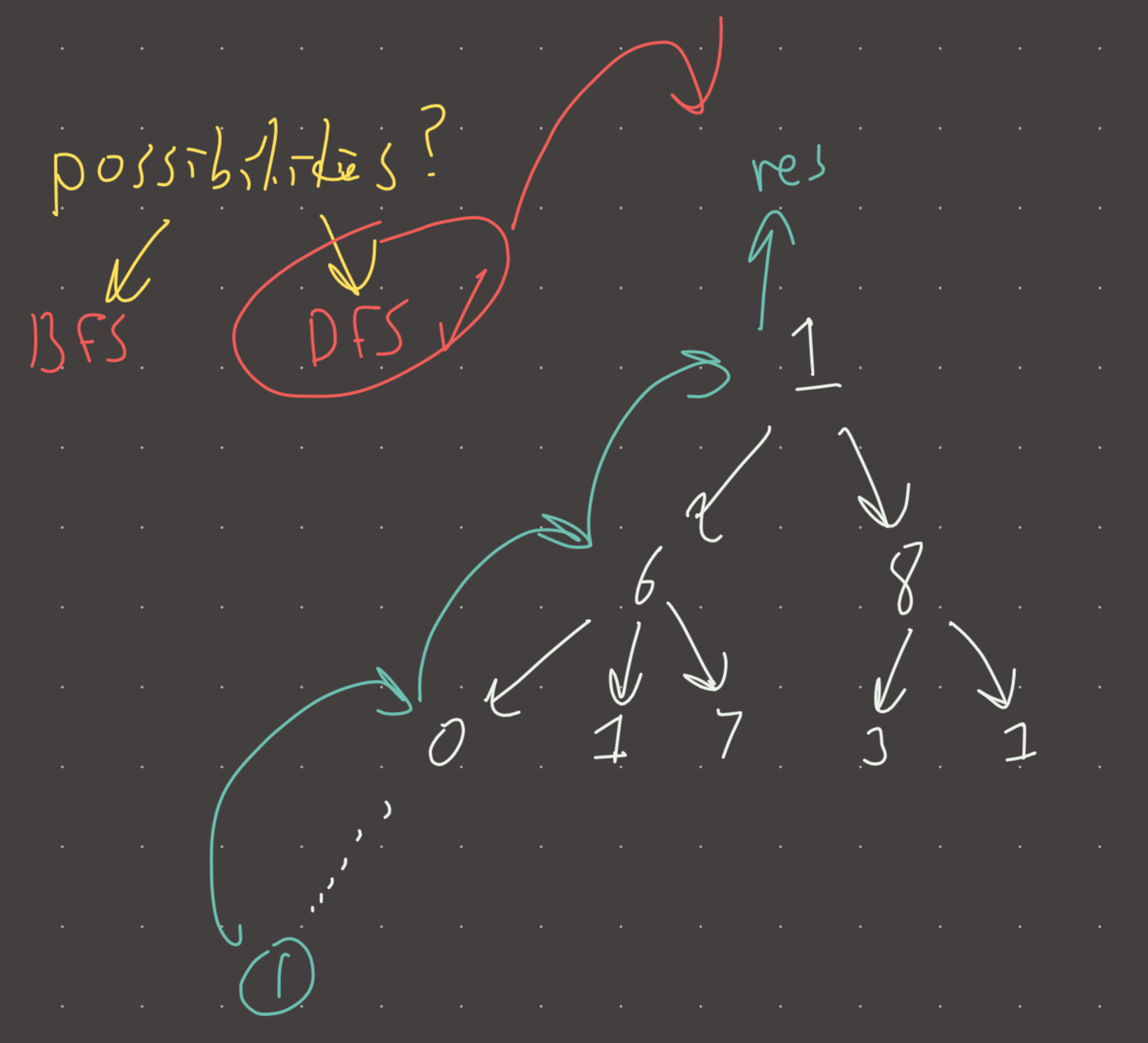
This is kind of a graph problem. Just do DFS with a cache for all possibilities and return 1 as the base case when length == n.

There is also a crazy math solution that I don’t really understand. Maybe memorize it if possible.

Implementation

def knight_dialer(n):
	moves = {
		1: [6,8],
		2: [9,7],
		3: [8,4],
		4: [3,9,0],
		5: [],
		6: [0,1,7],
		7: [6,2],
		8: [3,1],
		9: [2, 4],
		0: [6, 4]
	}
	@cache
	def dfs(prev, length):
		if length == n:
			return 1
		res = 0
		for move in moves[prev]:
			res += dfs(move, length +  1)
		return res
		
	res = 0
	for start_move in moves:
		res += dfs(start_move, 1)
	return res % (10**9 + 7)
		

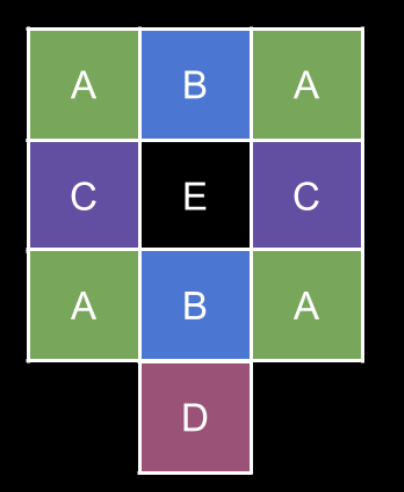
#this is the crazy math solution. The intuition revolves around treating numbers as groups group-to-group jump options are the same regardles of which number you start from in the group. I dont understand this but its worth to look a on a third revision
 
def knightDialer(self, n: int) -> int:
	if n == 1:
		return 10
	A = 4
	B = 2
	C = 2
	D = 1
	MOD = 10 ** 9 + 7
	for _ in range(n - 1):
		A, B, C, D = (2 * (B + C)) % MOD, A, (A + 2 * D) % MOD, C
	return (A + B + C + D) % MOD

This is the diagram from LC editorial:

Visual

Memory encoding

Review 1
As an experiment I wanted to see if this problem is possible with backtracking. Indeed it is but it results in TLE. Furthermore, when you take the current move out of the function, you can no longer cache it. A cacheable function must be a 2d DP dfs(move, length) because for example the move 3 at a length of 5 will have the same number of possibilities no matter what, so it make sense to process this only once and simply return the cached value upon future visitations (in this case visitations to (3, 5)).

review