Letter combinations of a phone number

Link: https://leetcode.com/problems/letter-combinations-of-a-phone-number/

Solution:

Topics: back tracking, DFS, grow

Intuition
Build out the combinations recursively and append them to the result. May be tempting to use for loops but the code is more complicated for no real gain…just keep it simple.

Implementation

def letter_combinations(digits):
	if len(digits) == 0:
		return []
	mapping = {
		'2': 'abc',
		'3': 'def',
		'4': 'ghi',
		'5': 'jkl',
		'6': 'mno',
		'7': 'pqrs',
		'8': 'tuv',
		'9': 'wxyz'
	}
	res = []
	def dfs(i, s):
		if i == len(digits):
			res.append(s)
			return
		for char in mapping[digits[i]]:
			dfs(i+1, s+char)
	dfs(0, '')
	return res
			
 
#time: o(n(4**n)) 
#NOTE: because there are at most 4**n combinations and each of them takes n time to build
 
#memory: o(n) stack space

Visual

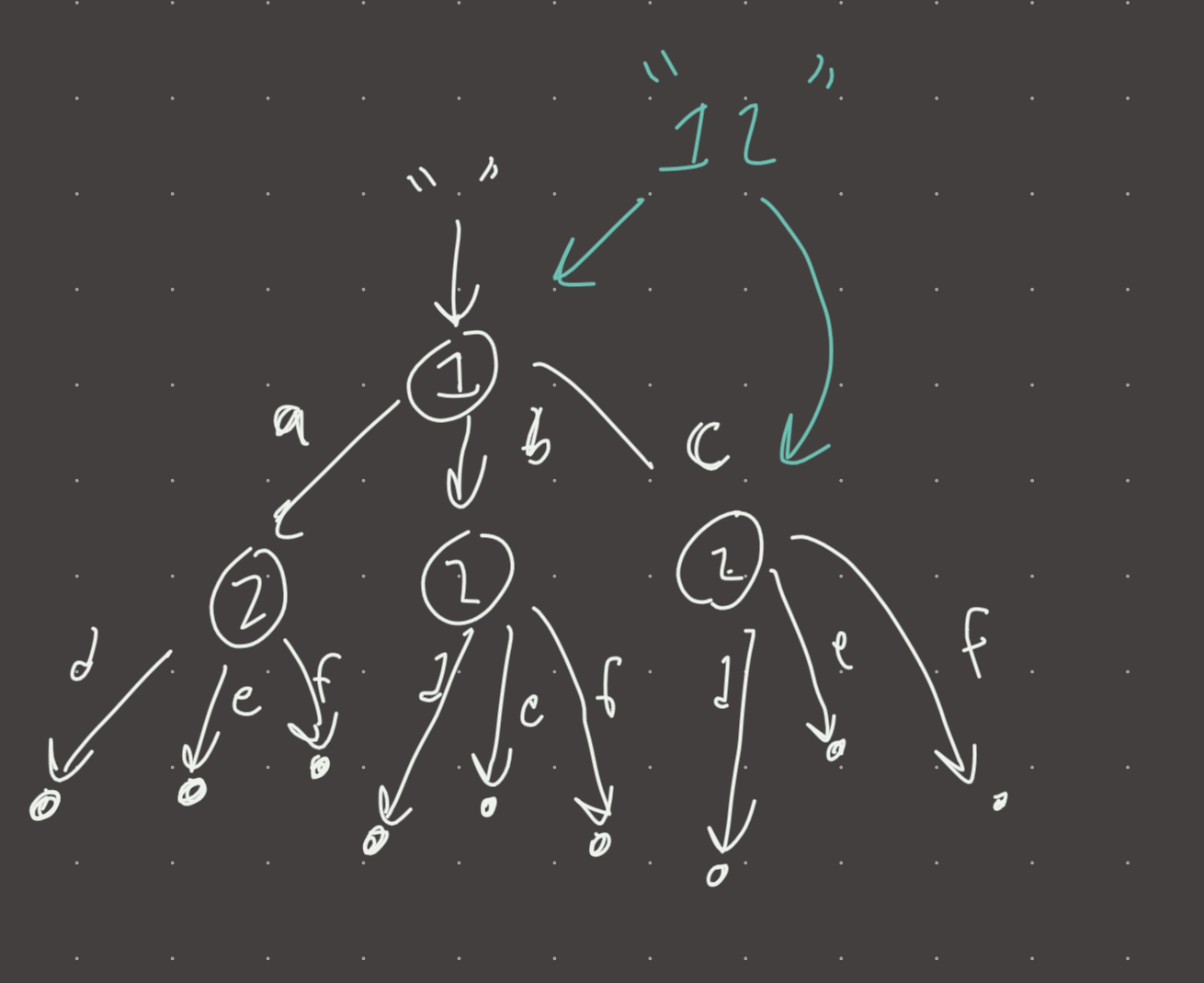
Review 1
The iterative solution is probably more intuitive:

Implementation (iterative)

def letter_combos(digits):
	if len(digits) == 0:
		return []
	mapping = {
		'2': 'abc',
		'3': 'def',
		'4': 'ghi',
		'5': 'jkl',
		'6': 'mno',
		'7': 'pqrs',
		'8': 'tuv',
		'9': 'wxyz'
	}
	
	res = ['']
	for num in digits:
		new_res = []
		for char in mapping[num]:
			for combo in res:
				new_res.append(combo + char)
		res = new_res
	return res

Note on the time complexity: Each digit can have at most 4 possibilities therefore the complexity is o(4**n) where n is the number of digits. Think in bits!

Review 2
This is actually a pretty fascinating problem because we have a choice: pure recursion or backtracking. Backtracking is actually the less efficient of the two because we must recurse search the same branch for every letter in every index i (we can get around this but it bloats the code because generally speaking backtracking relies on the state array at the leaf node rather than building results from the top down)! Of course with these constraints there is no difference at all but Its worth understanding the different approaches here:

Implementation (recursion)

def letter_combos(digits):
	if digits == '':
		return []
	mapping = {'2':'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':'wxyz'}
	def dfs(i):
		if i == len(digits):
			return ['']
		res = []
		combos = dfs(i+1) 
		#called only once per position i! 
	    #actualy we could put it in the for loop and cache the function...
	    #same thing but uses memory! 
		for char in mapping[digits[i]]:
			for combo in combos:
				new_combo = char + combo
				res.append(new_combo)
		return res
 
	return dfs(0)

I will implement back tracking properly here…this is the same as the first implementation but without the state propagation through the call stack.

Implementation (backtracking)

def letter_combos(digits):
	mapping = {'2':'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':'wxyz'}
	if digits == '':
		return []
	res = []
	state = []
	def bt(i):
		if i == len(digits):
			res.append(''.join(state))
			return
 
		for letter in mapping[digits[i]]:
			state.append(letter)
			bt(i+1)             #called for each letter and no way to cache!
			state.pop()
	bt(0)
	return res
		

This is of course a small nuance but it would make a huge difference under tighter constraints.

review