Longest duplicate substring

Link: https://leetcode.com/problems/longest-duplicate-substring/

Solution:

Topics: binary search, rabin-karp

Intuition
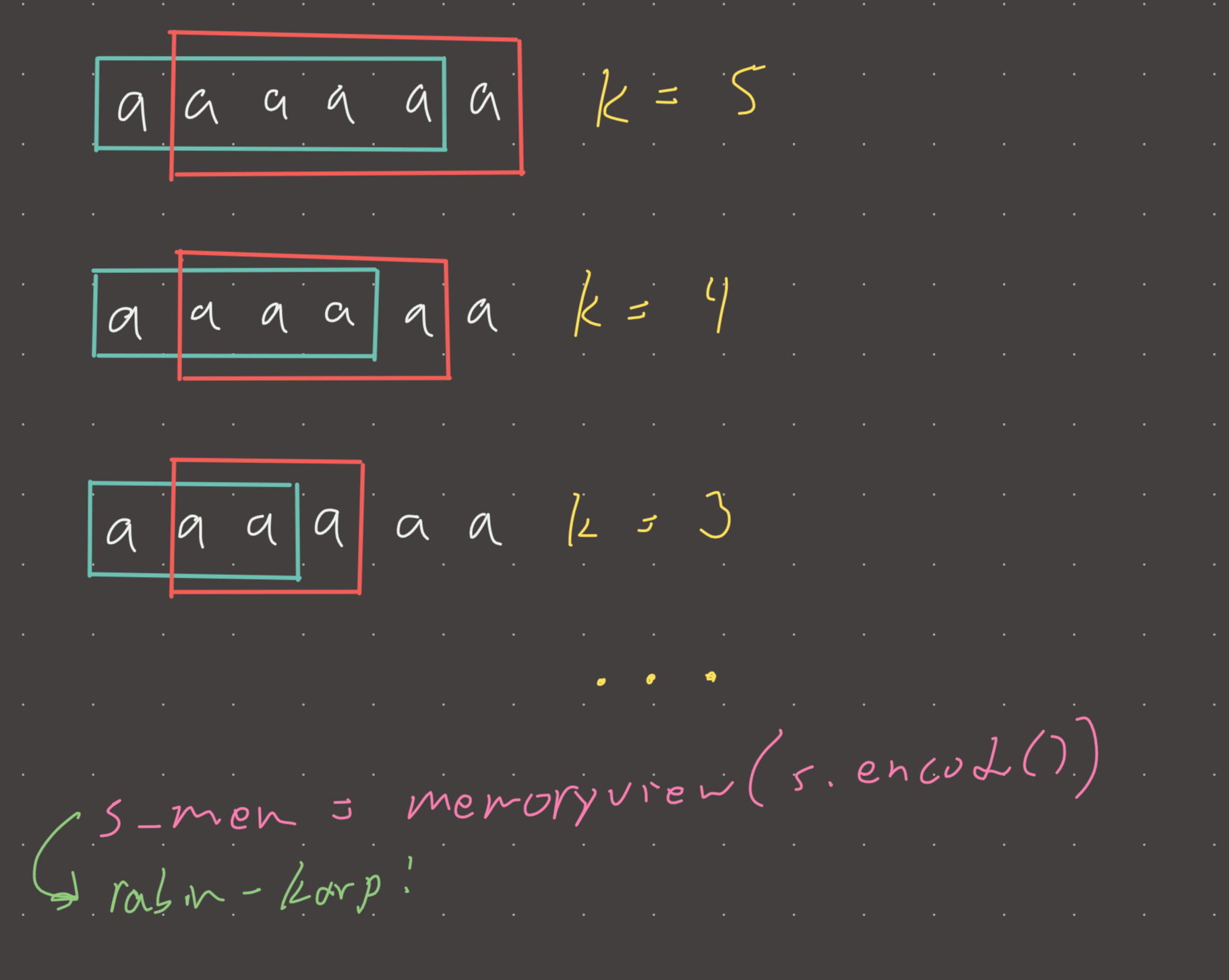
Very tricky problem. Binary search is used because if there exists a duplicate substring of length n, then there is guaranteed to be a duplicate substring of length n-1. The idea is to perform binary search with a sliding window to check if there exists a duplicate substring.

The optimal solution requires the rabin-karp algorithm because a simple sliding window and set requires slicing the string, and slicing is o(length) time complexity. Rabin-karp allows us to slice and hash a substring in O(1) time.

Rabin-karp is pretty complicated to code by hand, but python provides a very nice class memoryview that allows for O(1) slicing! The reason being is that when you slice the memoryview object, it does not create a new object, only a reference to the underlying data.

Implementation

def longest_dup(s):
	def has_dup(length):
		has = set()
		l = 0
		for r in range(length, len(s)+1):
			curr = s_data[l:r]
			if curr in has:
				return s[l:r]
			has.add(curr)
			l += 1
		return ''
 
	s_data = memoryview(s.encode()) #remember this!
	res = ''
	l = 1
	r = len(s)-1
	while l <= r:
		mid = (l + r) // 2
		dup = has_dup(mid)
		if len(dup):
			l = mid + 1
			res = dup if len(dup) > len(res) else res
		else:
			r = mid - 1
	return res
	
#time: o(nlogn)
#memory: o(n)

Visual

Review 1
Nice problem. I actually came up with a pretty clever and somewhat o(n*n) solution using a trie search…unfortunately this approach results in MLE. I forgot that we must use rabin-karp and binary search for this class of problems. Use memoryview(s.encode()) for o(1) slicing. TODO: learn how to implement rabin-karp rolling hash from scratch.

review
hard