Link: https://leetcode.com/problems/maximal-square/
Solution:
Topics: Bottom-up DP
Intuition
This is unquestionably a very tough problem because by far the most intuitive approach is Bottom-up DP. Unfortunately, I tend to favour top-down DP in most cases except for problems requiring kadanes algorithms. Because of this, I struggled quite a lot with this one.
The key here is to traverse the matrix and keep track of the largest square we can make with the current cell. How do we do this? Lets look at an example:
1 1
1 1
^
Lets start at position 1,1
Clearly this is a square of side length 2 and area 4, but how can we know for sure?
Well, we can check all three adjacent cells to check! They are all 1's so we have a valid square.
1 1 1
1 1 1
1 1 1
Lets look at the above example and start at (1, 1). This sub-square has a side length of 2...so we can store that result in the current position!
1 1 1
1 2 1
1 1 1
Lets move to (1, 2). If we look at the original matrix, we can also make a square of side length 2...so lets record that result.
1 1 1
1 2 2
1 1 1
At (2, 1), also a square of side length 2...
1 1 1
1 2 2
1 2 1
At (2, 2), a square of side length 3..
1 1 1
1 2 2
1 2 3
So what is the algorithm? If we reach a cell with 1, we must simply check to see if it can be part of a square that has been made previously! So this would be the min of the cell up, the cell right and the cell in the upwards diagonal! And we add 1 to that because we are extending the square!
We must take the min of the 3 adjacent cells because, by definition the min is the upper bound for the square side-length:
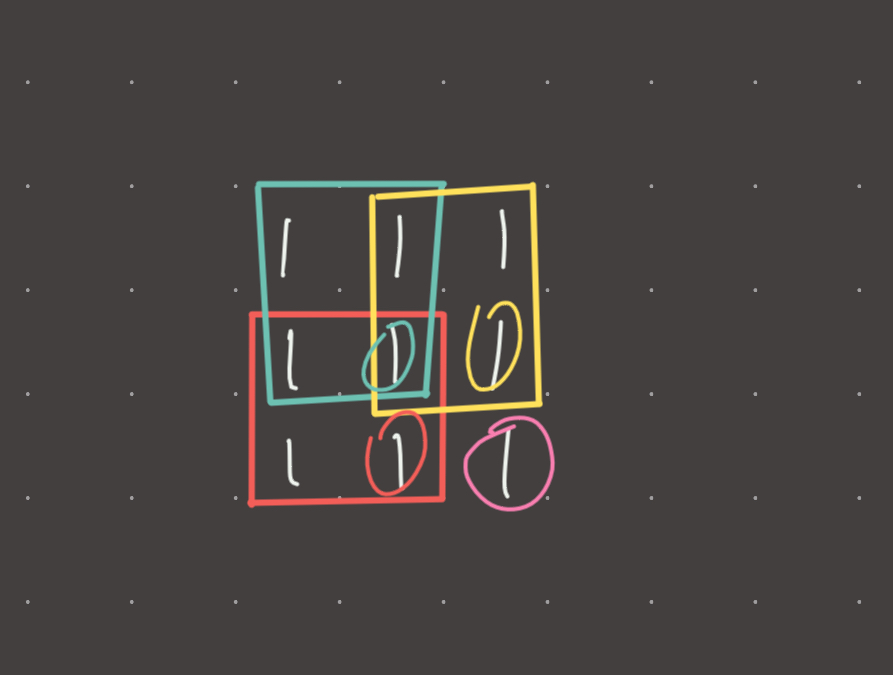
Take a look at position (2, 2). We know that it can complete a square of side-length 3 because each of the 3 adjacent cells can themselves complete a square of at least length 2!
Lets look at a counter-case:
Starting again from position (2, 2), we can see that the top adjacent cell can only complete a square of size 1… because its own top adjacent cell has a value of zero. This means that (2, 2) cannot complete a square of size 3. Thus the minimum size square that any of the adjacent cells can complete is the upper bound of the size for the new square!
Conceptually, this can be thought of as building squares as we go, using squares that we have previously built.
The implementation is pretty straight forward, but we must make sure that there is always a value to read at dp[row-1][col] and dp[row][col-1] and dp[row-1][col-1].
Implementation
def max_square(matrix):
res = 0
dp = [[0]*(len(matrix[0])+1) for _ in range(len(matrix)+1)]
for i in range(1, len(dp)):
for j in range(1, len(dp[0])):
if matrix[i-1][j-1] == '1':
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
res = max(res, dp[i][j])
return res * res
#time: o(nm)
#memory: o(nm)Mnemonic
You are team captain on a 4 man team of soccer. Your team is only as strong as your weakest player, so the overall team strength is the strength of the weakest player.
Visual
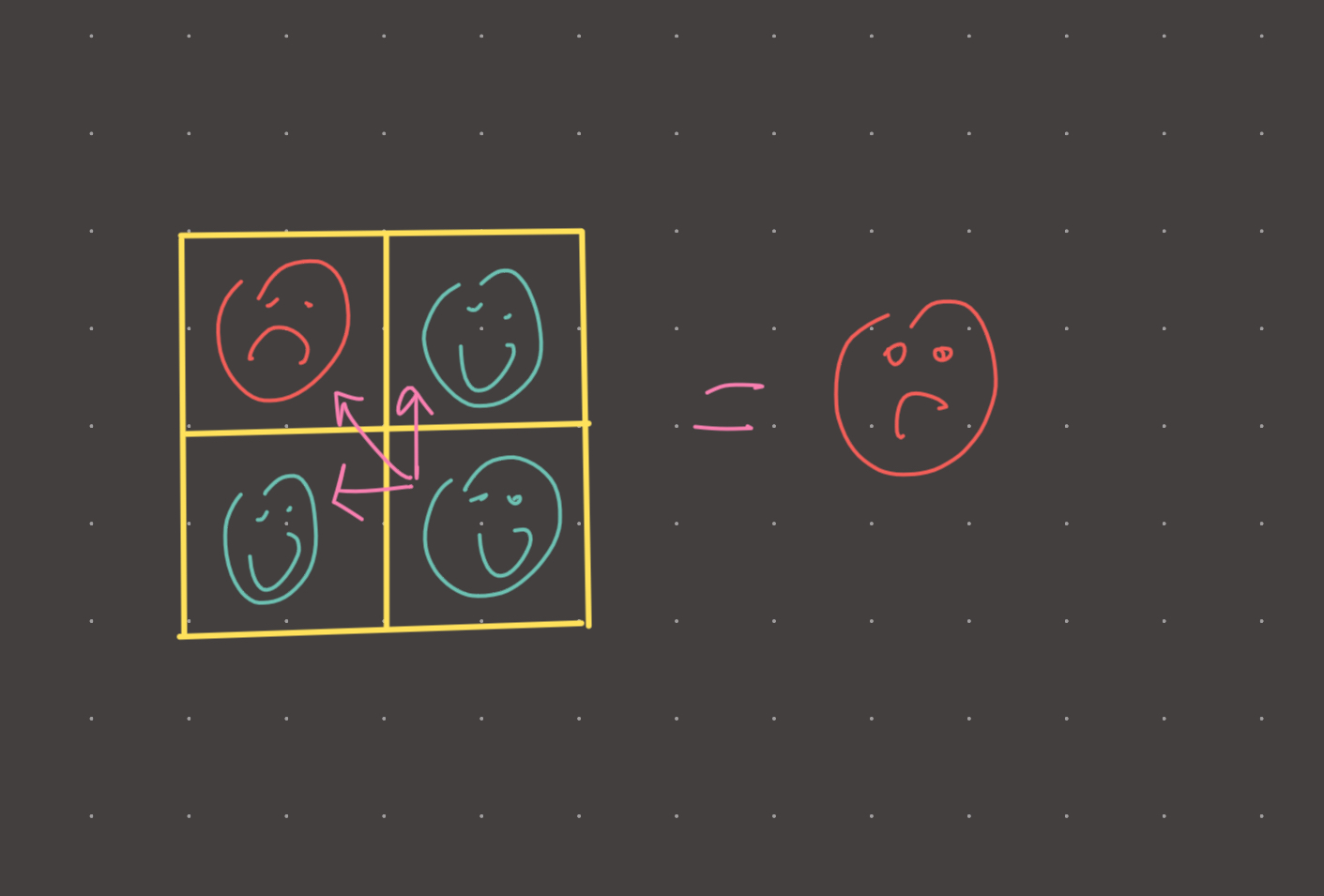
Review 1
Had no issues with this one. Great DP problem. Progress! I think I prefer the two pass constant space solution.