Link: https://leetcode.com/problems/maximize-score-of-numbers-in-ranges/
Solution:
Topics: binary search, Heaters
Intuition
This is a fantastic binary search problem. The problem statement is very difficult to decipher and I initially began thinking about it as purely a greedy interval problem. The key idea is to use binary search to jump across the sorted intervals. But here is the trick: we can’t over-jump. Over-jumping is akin to skipping over an entire interval, which is not permitted (ith integer must be in the ith interval).
This problem is somewhat similar to Heaters, in the sense that in the Heaters problem we can search for a radius that will reach all houses. This problem is similar, except we search for a score that permits us to select an integer at every interval without skipping over any!
For example:
[0, 3, 6] d=2
this represents the intervals (0, 2), (3, 5), (6, 8)
if we choose a score of 6, we can see that in the best case we choose 0 as the first integer, and then we must choose 6 as the next integer (0+6). We can see that by doing so we have skipped over the range (3, 5)! so this is an invalid score.
It’s very tricky to recognize this as a binary search problem but the key intuition is that chosen integers will be at least x apart, but can be more than x apart if the intervals are not overlapping. If the integers are more than x apart, this makes no difference to the result because we are after the minimum absolute difference. Or in other words, you will have two intervals with a difference that is greater than x; this does not matter because we constrain x to a lower bound.
This makes sense because if we use x directly to jump to the next interval, this ensures that the abs(chosen1-chosen2) is the minimum for the entire set of integers chosen (assuming the ranges are in sorted order).
A key observation that must also be made is that we must always choose the first integer in the sorted set of starts start[0]. Why is this the case? This is to ensure that we have the maximum possible space available to us to insert the score.
For example:
[0, 3, 6] d=2 score=4
We can chose 0, 4, 8 for a score of 4. All chosen are in range.
Lets chose 1, 5, 9 for a score of 4. Notice that 9 is not in range!
Basically, by choosing an integer > start[0] for the first chosen, we block ourselves off from ranges that we may need.
We can think about it in terms of intervals:
012345678 --> possible integers for the range [0, 3, 6] d=2
^
take 0, eight possible integers remaining
012345678
^
take 1, seven possible integers remaining!
Essentially, we start by choosing the first integer and then add the score to it to see if we overshoot the next interval or not. If we don’t overshoot, we choose start[i] if there is no overlap, or prev+score in the case of an overlap.
Some further thoughts on the problem solving here… This problem was extremely difficult for me, and indeed it’s a very difficult problem. The problem statement is very confusing, and I wasted quite a lot of time thinking about it. It would have been helpful here to forget about the problem statement and just analyze the example cases to see the obvious pattern:
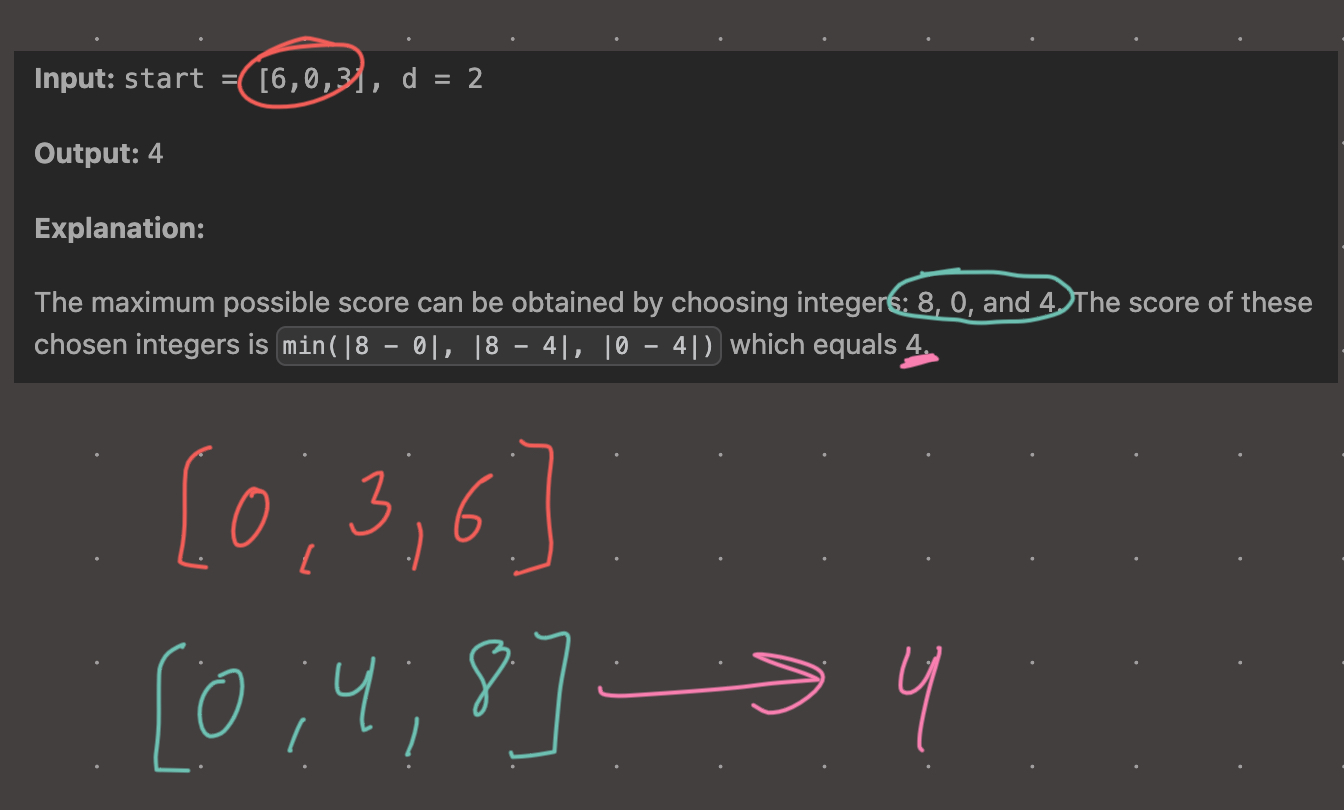
The chosen integers are all no less than 4 apart, thus the max score is 4. In this case there is an overlap interval. 0+4 = 4, so for interval i=1 we take 4 instead of 3.
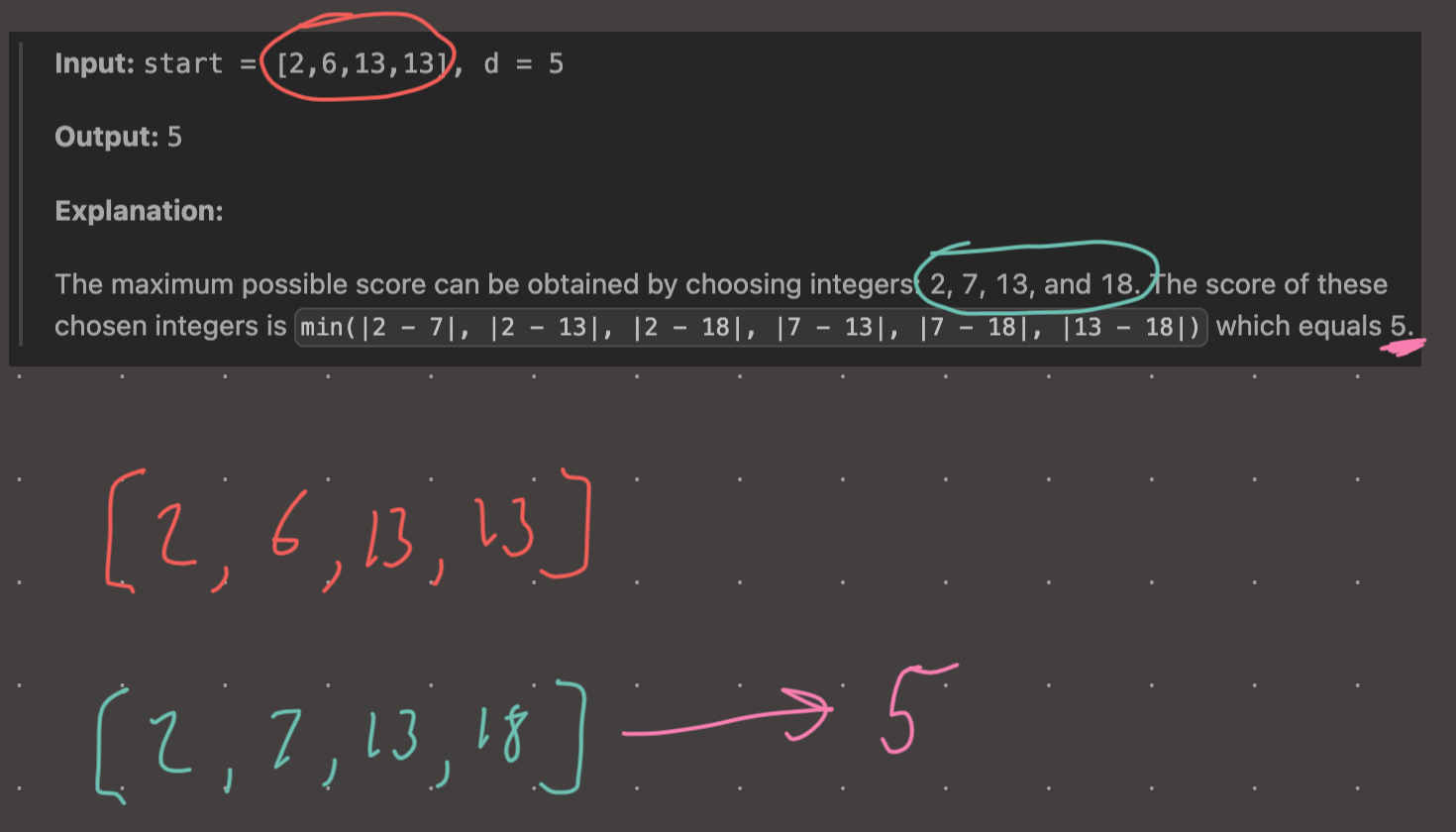
The chosen integers are all no less than 5 apart, thus the max score is 5. In this case we can see that there is an example of a disjoint interval because 7+5 is 12…but 13 gets selected because its the minimum integer for i=2.
Implementation
def max_score(start, d):
start.sort()
def is_valid(score):
prev = start[0]
for i in range(1, len(start)):
if prev + score > start[i] + d: #overshoot case
return False
prev = max(prev+score, start[i]) #choose prev+score in case of
return True #in case of overlap
l = 1
r = start[-1] + d
while l <= r:
mid = (l + r) // 2
if is_valid(mid):
l = mid + 1
else:
r = mid - 1
return l - 1
#time: o(nlogn)
#memory: o(1)Visual
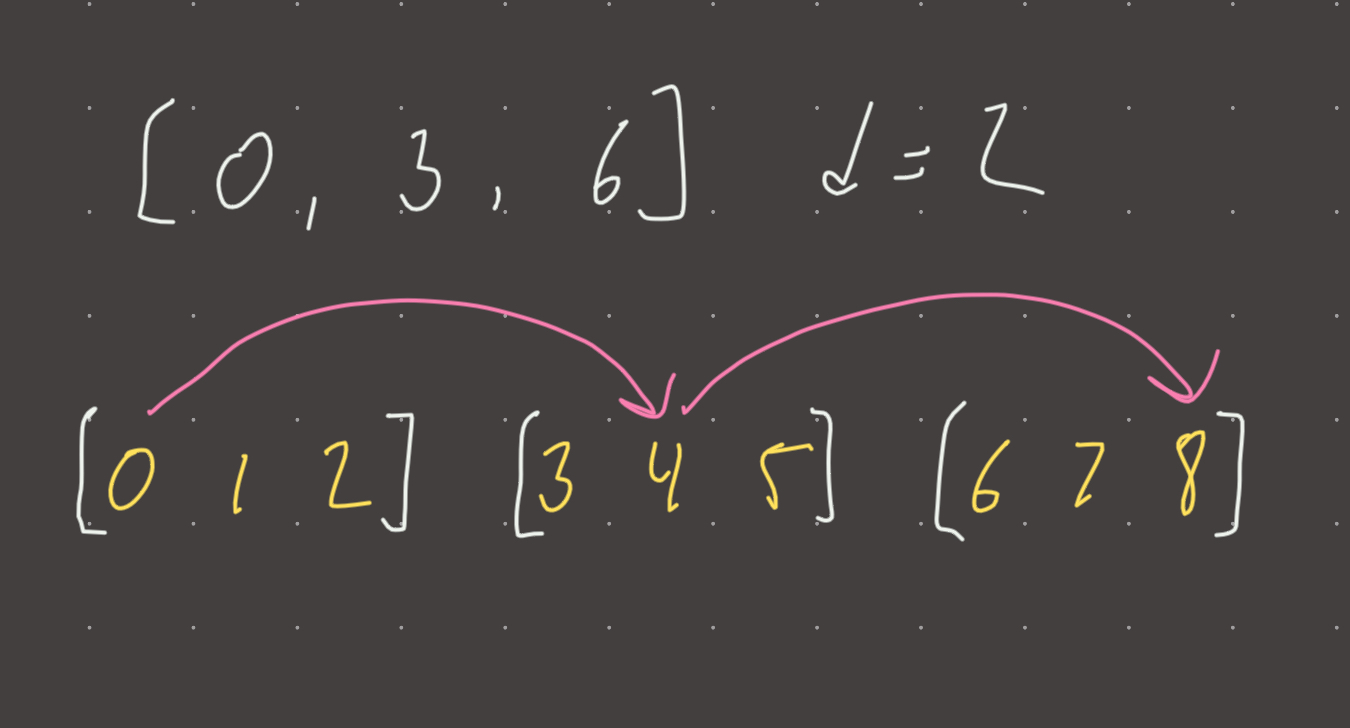
Review 1
Even having seen this problem before, it still took me some time to re-understand it! Its very confusing in the sense that we are after the the maximum minimum difference. Thats hard to wrap your head around! I got more insight into this on the second time around.
Lets put the intervals on a number line:
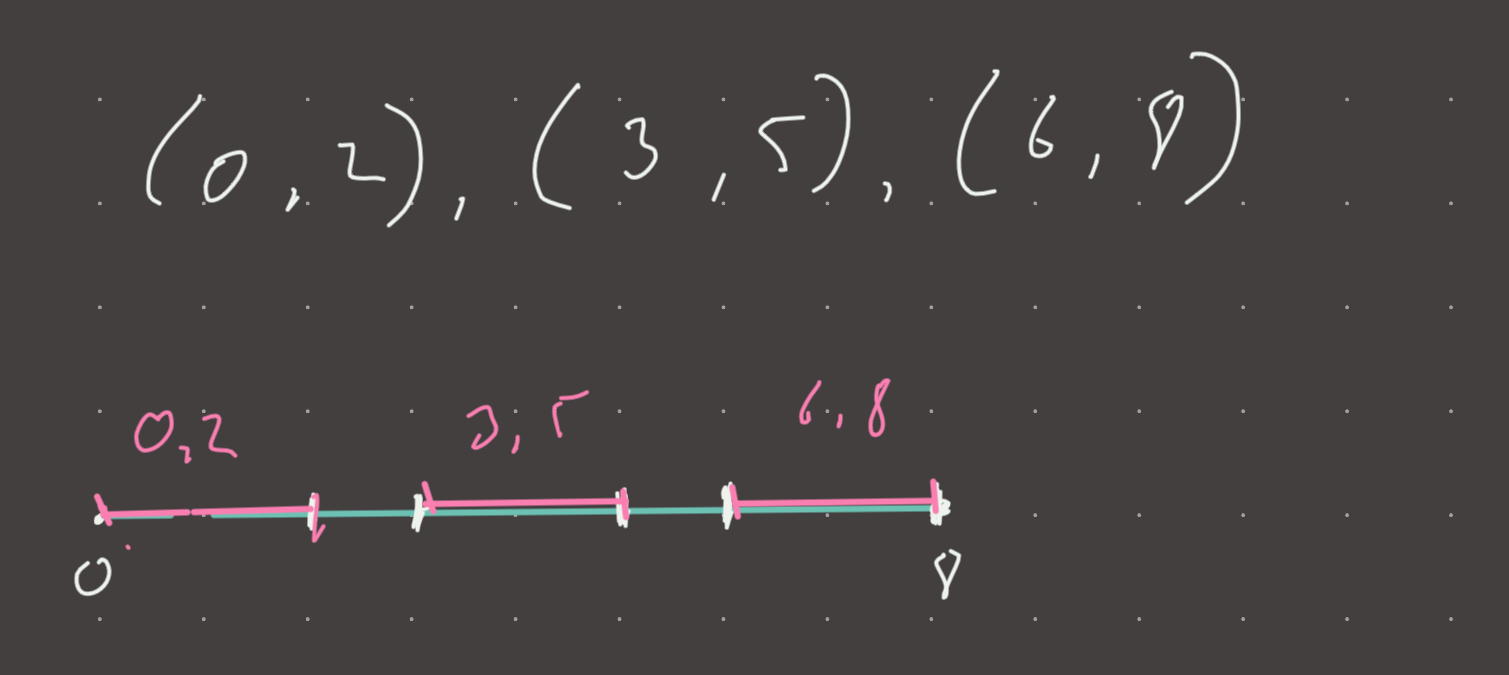
Lets now set score to 0:
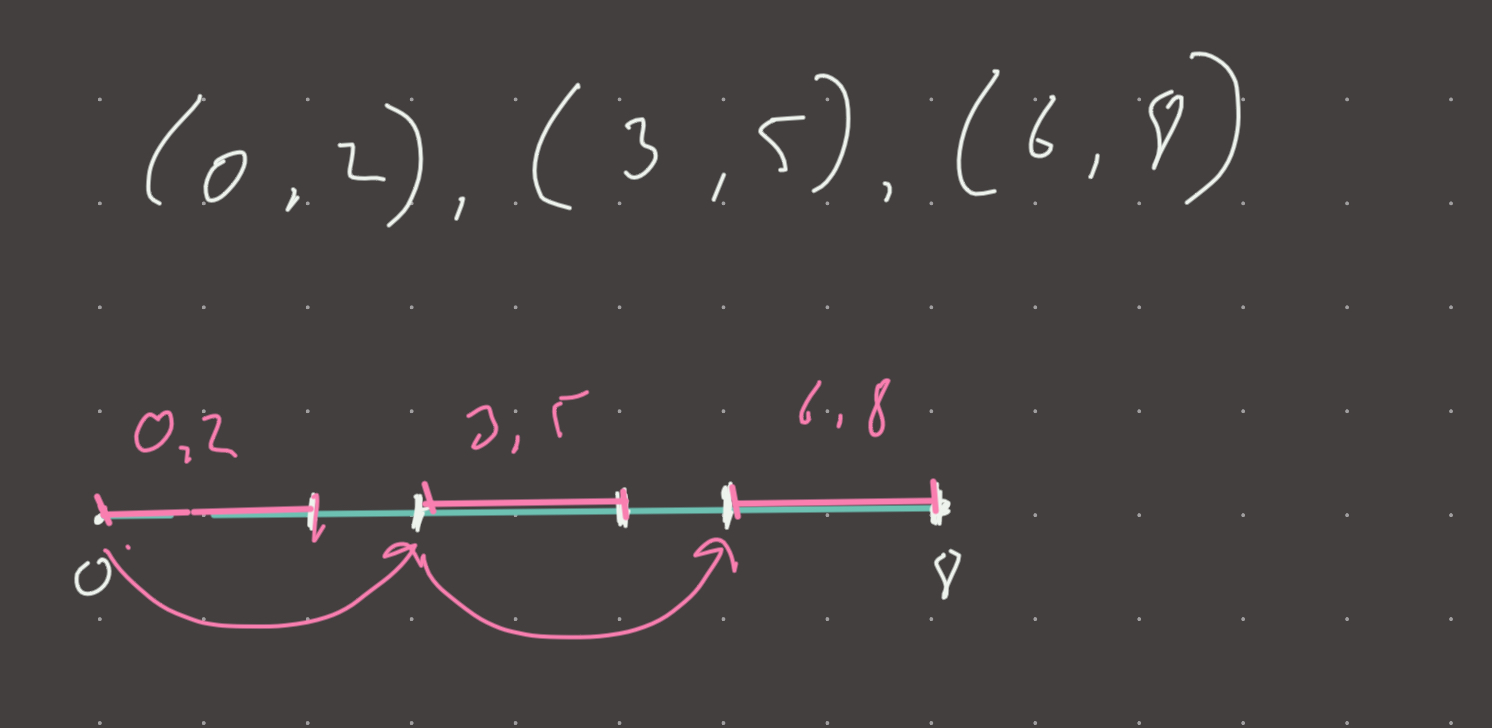
Setting a score of zero is equivalent to choosing the start of every interval. In this case, we choose 0, 3, 6. This is indeed a valid choice as all these selections are guaranteed to be in range.
Lets set the score to 1:
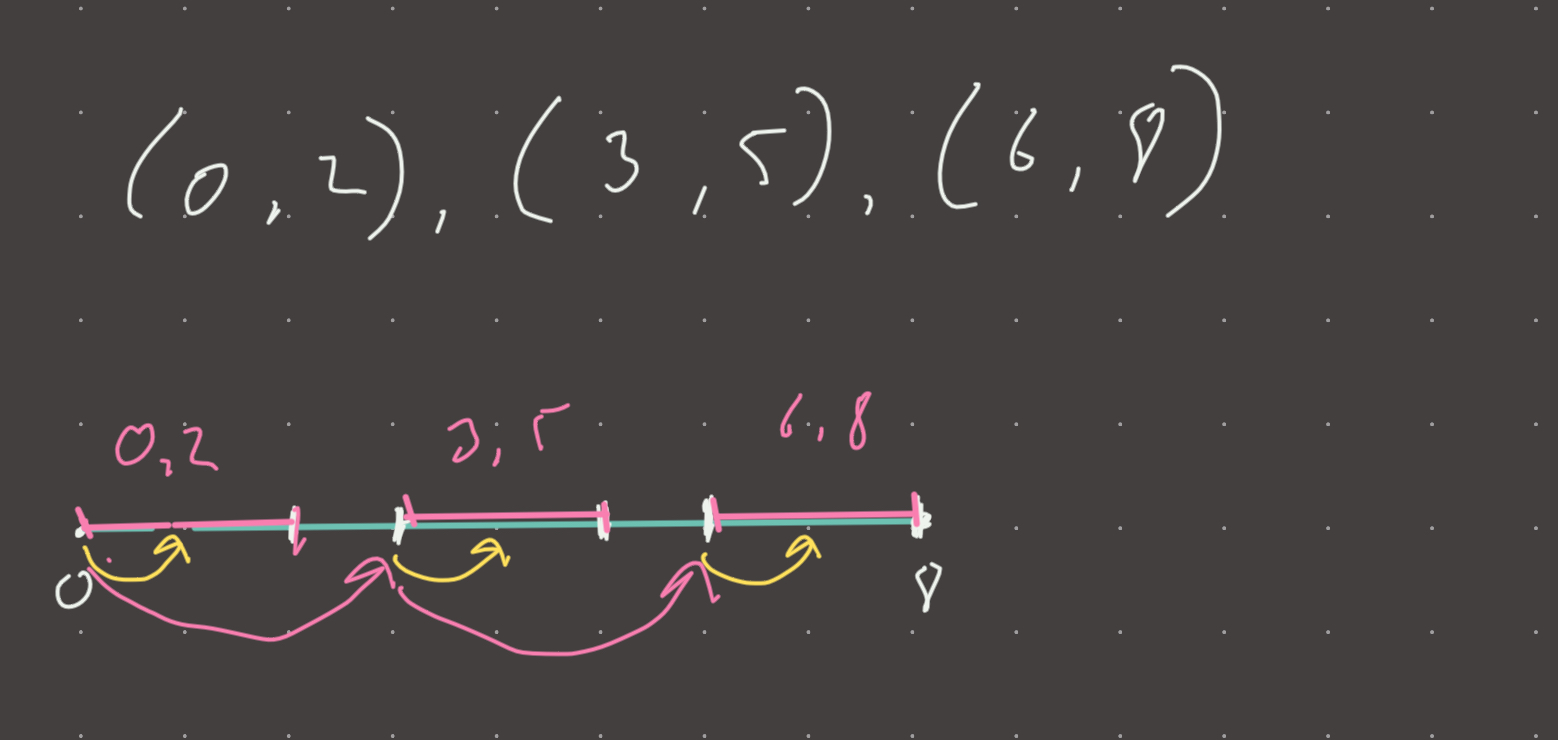
Setting the score to 1 represents the exact same traversal through the intervals as 0. Why? Because if increasing the start interval by the score is less than the start of the next interval, we take the start of the next interval!
Set the score to 2:
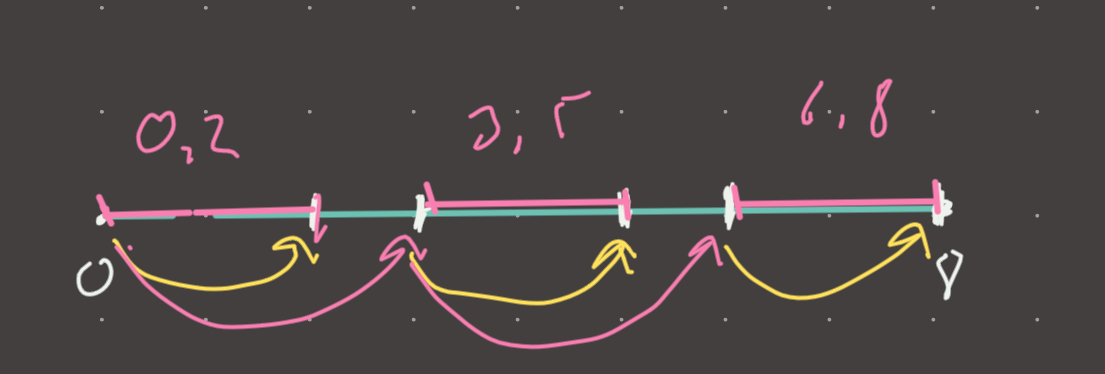
Again, this represents the same traversal as 0, 1.
Set score to 3:
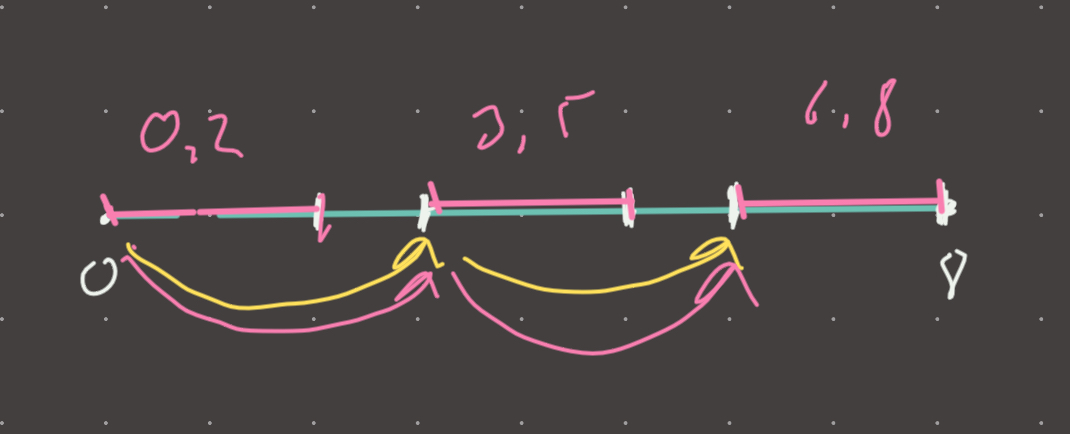
Same as 0, 1, 2.
Set score to 4:
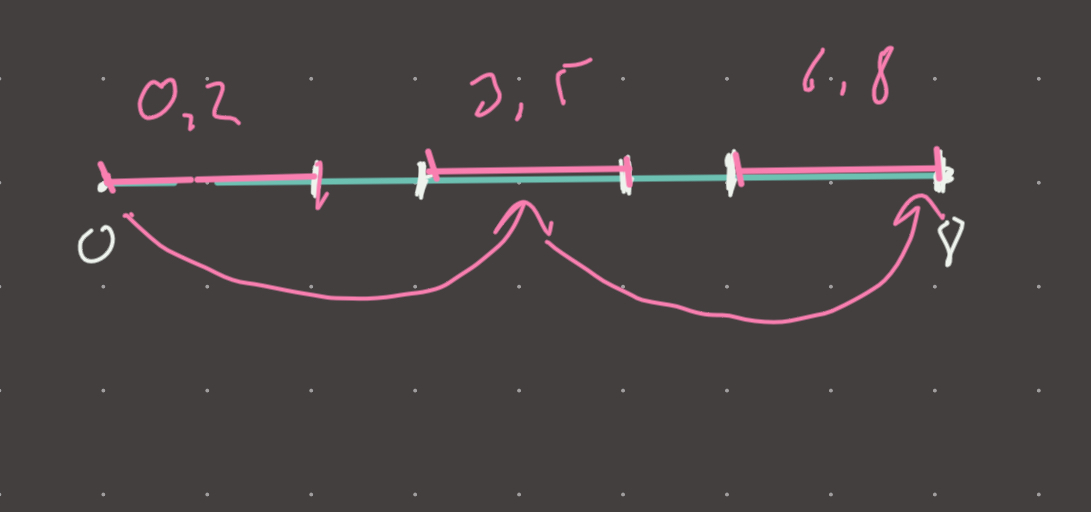
We have a new max score of 4! We chose 0, 4, 8 and all are in range!
Set score to 5:
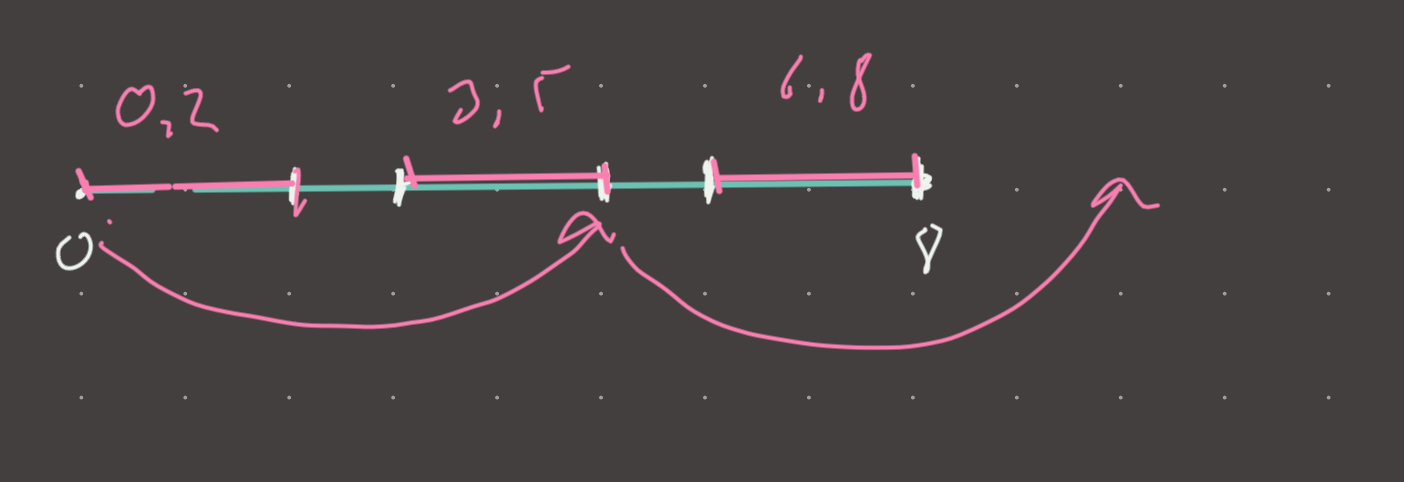
We chose 0, 5, 10! By choosing 10, we have overshot the last interval! So 5 and every score above it is invalid. We end with a max-score of 4!
This problem is ultra confusing in the way it is formulated, but we can restate it as such: What is the maximum jump we can make through the intervals such that no interval is over-shot. Under-shooting is allowed.
How do you make the connection from “minimum difference” to “jumps”? Well if you think about it, the size of a jump x guarantees that no two numbers landed on (chosen) will be less than x apart. Admittedly, this is a subtle connection.
Review 2
Took a few minutes of thinking, but I solved this without too many problems.