Maximum number of alloys

Link: https://leetcode.com/problems/maximum-number-of-alloys

Solution:

DSA: binary search

Intuition
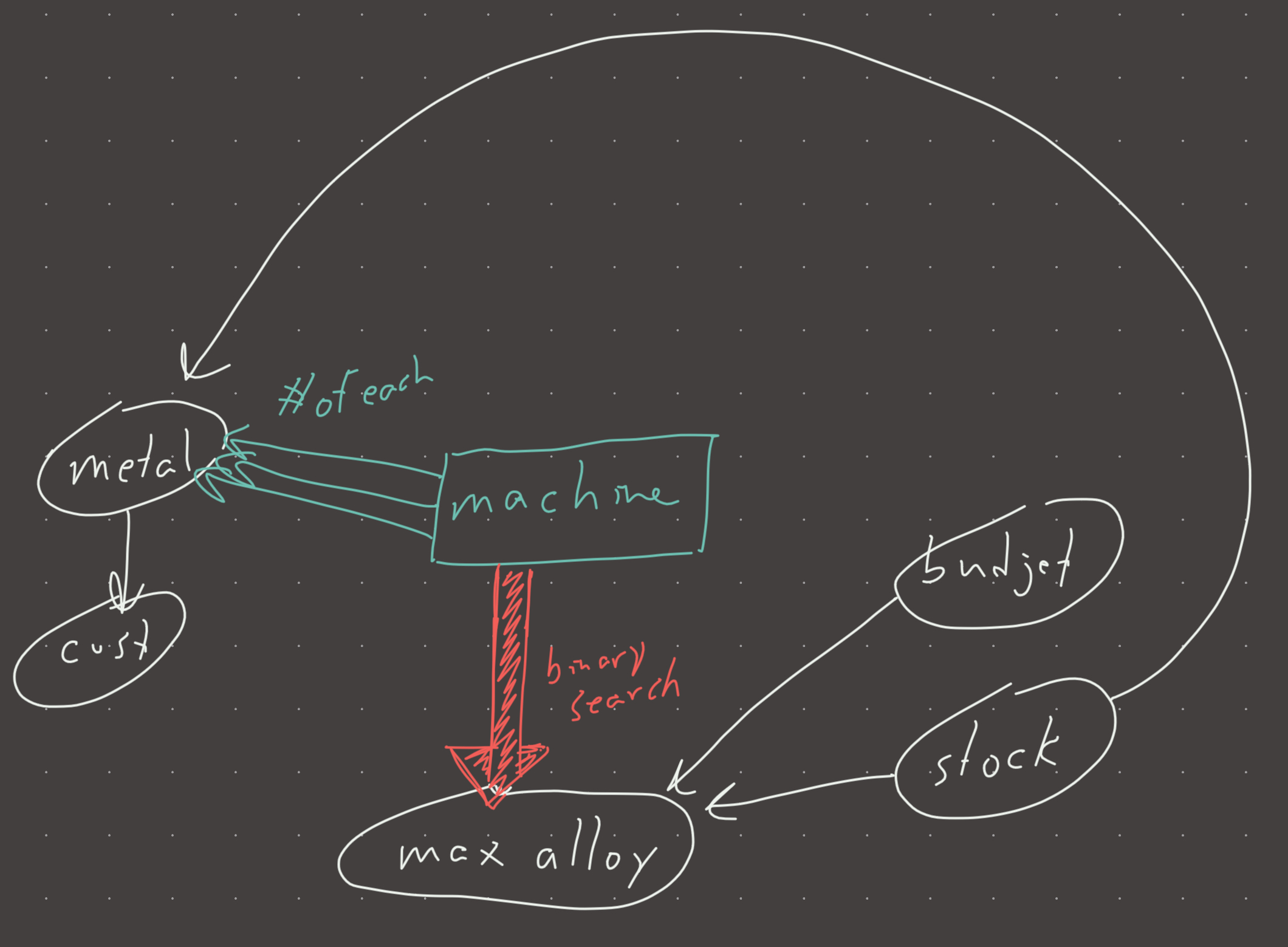
The key to this problem is understanding that if we can make X alloys with a machine, then we can also by definition make X-1 alloys with that machine. Since the number of alloys made has this monotonic property, we can perform binary search on a range of 1 alloy to max alloys for each machine to get our result.

The upper bound of alloys is a bit tricky, but logically it cannot be more than sum(stock)+budget if we assume the best case of a composition of all 1’s.

It may be tempting to simulate each alloy being created iteratively, but this results in TLE and with some simple math, we can compute if a machine can create X many alloys in O(len(compostion[i])) time instead of O(qty) time. The key is to compute the total number of each metal needed is to determine the number of each metal needed (metal * qty) and subtract the stock. Then if the number of metals needed is greater than zero, we multiply that by the respective cost and add that to total cost. If the total cost is smaller than the budget, we can create that quantity. If we can create that quantity with even a single machine, we then move our binary search towards the upper bound.

Implementation

def max_alloys(composition, stock, cost, budget):
	def can_make(qty, machine):
		total_cost = 0
		for i, metal_needed in enumerate(machine):
			metal_needed = metal_needed * qty - stock[i]
			metal_needed = metal_needed if metal_needed > 0 else 0
			total_cost += metal_needed * cost[i]
		return total_cost <= budget
 
	def bs(machine):
		machine_max = 0
		l = 1
		r = budget + sum(stock)
		while l <= r:
			mid = (l + r) // 2
			if can_make(mid, machine):
				machine_max = mid
				l = mid + 1
			else:
				r = mid - 1
		return machine_max
 
	res = 0
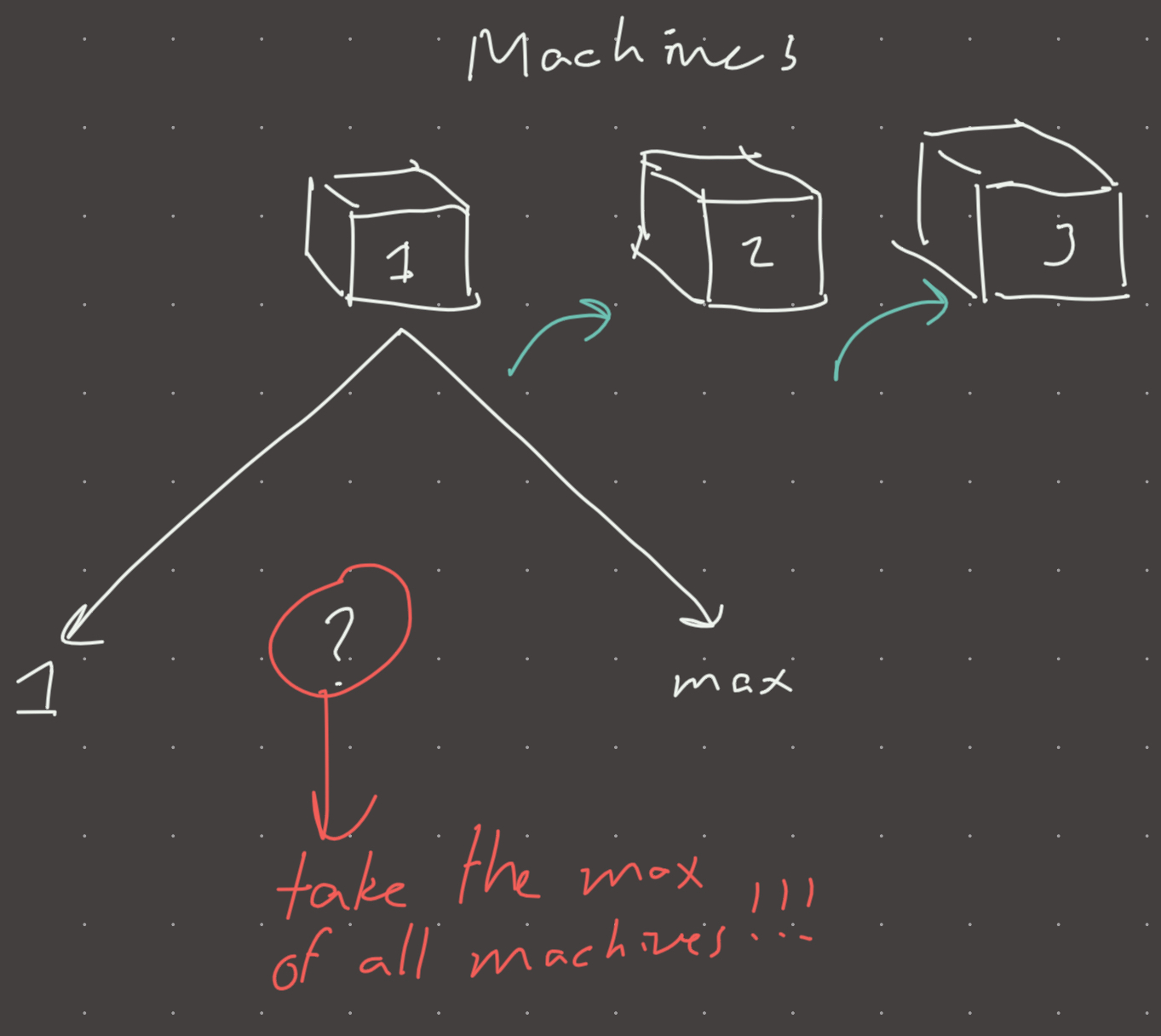
	for machine in composition:
		res = max(res, bs(machine))
	return res

Visual

Review 1
Nice binary search problem. Just perform a binary search for each machine on the number of alloys that can be created while staying under budget. Take the max of all.

review