Maximum subarray

Link: https://leetcode.com/problems/maximum-subarray/

Solution:

Topics: kadanes, subarray

Intuition
This problem is a classic application of kadanes greedy algorithm. Not really much to this problem if you understand how kadane’s works. The idea is that if the current subarray sum added to the next element is smaller than the next element, we can discard the current subarray sum because it cannot be part of the maximum subarray.

Its important to note that negative numbers can be part of the max subarray given that they connect positive sum subarrays together.

For example:

[1,2,3,4,-1,1,2,3,4]

-1 is part of the maximum subarray because it connects the subarrays [1,2,3,4] and [1,2,3,4] for a max subarray sum of 19

Implementation (DP table)

def max_subarray(nums):
	dp = [0] * len(nums)
	dp[0] = nums[0]
	res = nums[0]
	for i in range(1, len(nums)):
		dp[i] = max(nums[i], nums[i] + dp[i-1]) 
		res = max(res, dp[i])
	return res
 
#time: o(n)
#memory: o(n)

Implementation (Optimized DP)

def max_subarray(nums):
	curr_sum = nums[0]
	res = nums[0]
	for i in range(1, len(nums)):
		curr_sum = max(nums[i], nums[i] + curr_sum)
		res = max(res, curr_sum)
	return res
 
#time: o(n)
#memory: o(1)

Visual

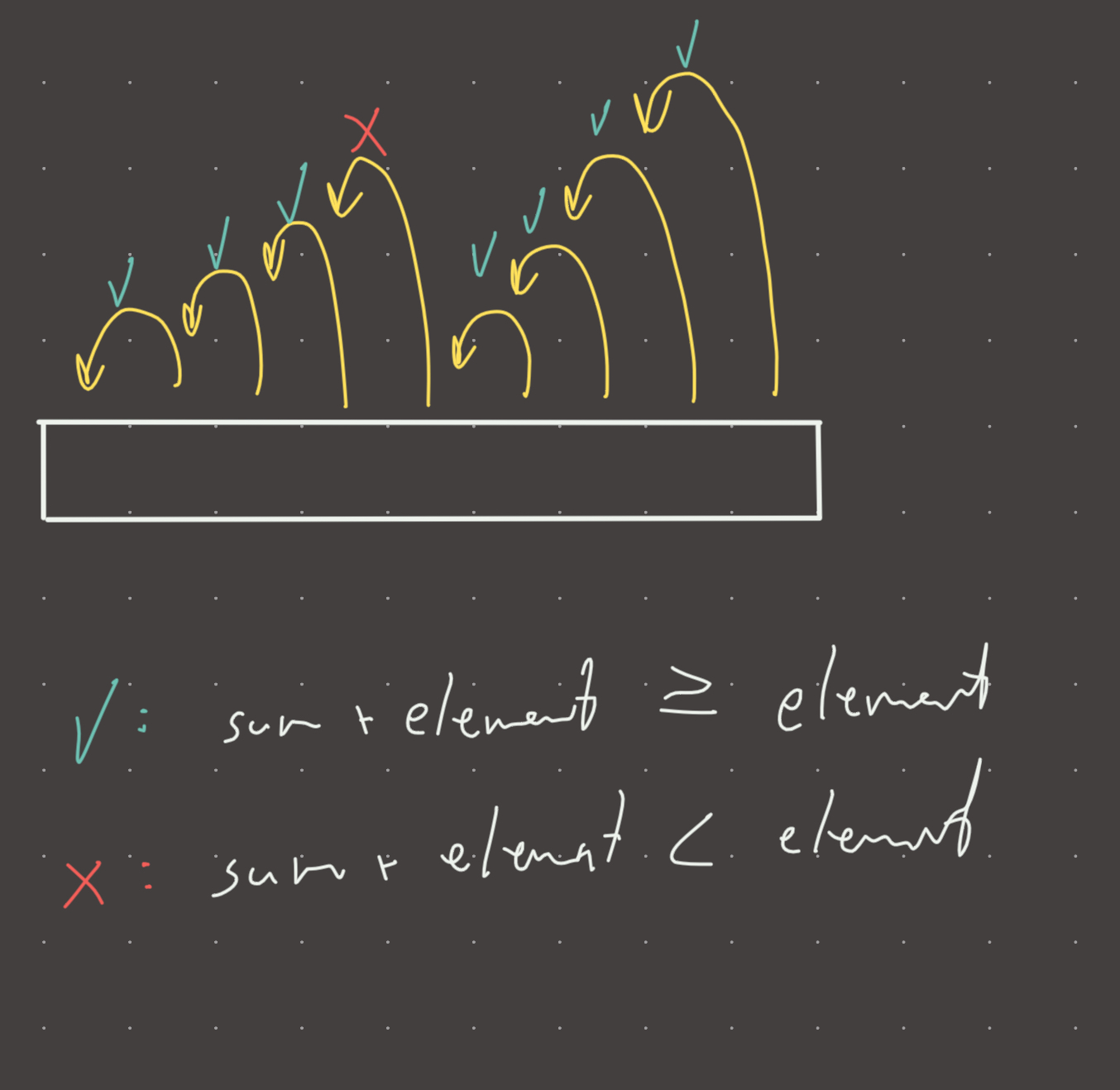
Review 1
Classic Kadane’s algorithm. I prefer this implementation:

def max_subarray(nums):
	res = float('-inf')
	curr = 0
	for num in nums:
		curr = max(curr+num, num)
		res = max(res, curr)
	return res

review