Link: https://leetcode.com/problems/maximum-subarray-sum-with-one-deletion/
Solution:
Intuition
This one was tough to wrap my head around. To solve for the maximum subarray without deletions we can use kadane’s algorithm, and a naive approach would be to set each index to zero and run kadane’s n**2 times (and take the max). Of course this would be highly inefficient. So we have to figure out a more clever way. How?
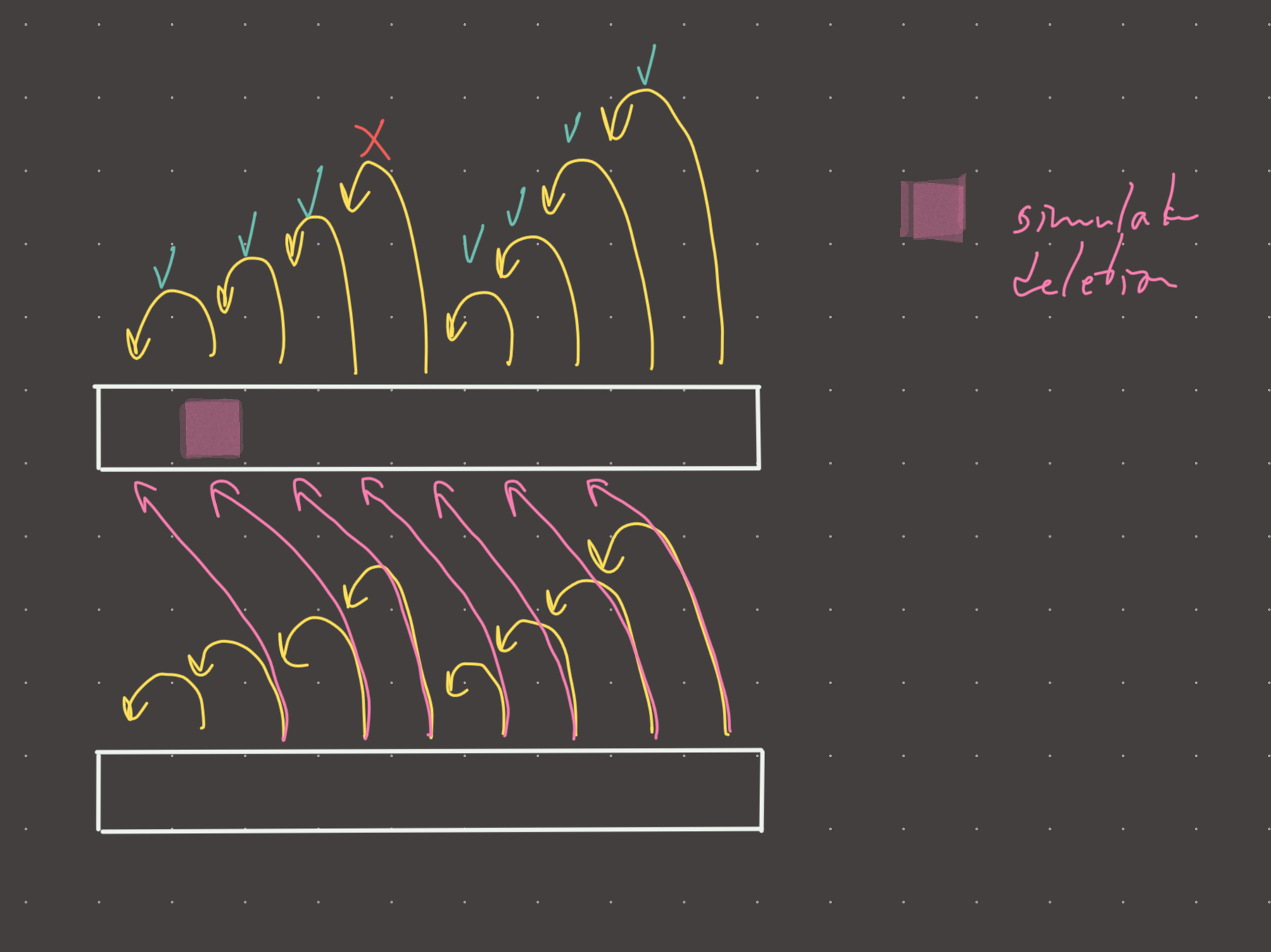
There is actually a way to use two DP arrays (like in regular kadane’s) to simulate a deletion at each index. One array is unmodified (regular kadanes), and the other allows deletions by referencing the unmodified array! It’s important to keep one array unmodified because we are only allowed one deletion, so a reference to the original must exist.
The implementation is very tricky, but the gist of it is that when we use regular kadane’s, we compare the current element against dp[i-1]…and to simulate a deletion, we can instead compare against dp[i-2] and store that result in the array that allows for deletions!
So at each index, we are comparing the modified against the previous unmodified! And because this comparison always references the unmodified kadane’s, we can never simulate more than one deletion.
Implementation
def max_subarry(arr):
without_del = [0] * len(arr)
with_del = [0] * len(arr)
without_del[0], with_del[0], res = arr[0], arr[0], arr[0]
for i in range(1, len(arr)):
without_del[i] = max(without_del[i-1] + arr[i], arr[i])
with_del[i] = max(with_del[i-1] + arr[i], arr[i])
if i >= 2:
with_del[i] = max(with_del[i], without_del[i-2] + arr[i])
#simuate the deletion of element at i-1
res = max(res, with_del[i])
return res
#time: o(n)
#memory: o(n)Visual
Review 1
Super tricky problem, but I was able to solve it partially from memory. Basically we run two kadanes algorithms simultaneously (but with arrays). One array is the a pure kadane’s, the other allows for deletions. We simulate deletions by comparing the current element in the modified array to the previous-previous element in the pure kadanes array!
This way, we can enforce at most one deletion due to the fact that we “rebase” ourselves with the original…or we simply continue the sequence if deletion is not profitable.