Link: https://leetcode.com/problems/median-of-two-sorted-arrays/
Solution:
Topics: binary search
Intuition
Insane problem. I actually found an o(logn*logm) solution by searching for “what position would I be in if the array was sorted”. We would binary search through nums1 and for every position mid we simply search for that element in nums2. We do both a leftmost and rightmost search. If mid + leftmost == median_pos or mid + rightmost == median_pos, then we return nums1[mid]…and of course handle all the edge cases (which are numerous).
There is a far more clever solution though that is o(log(n+m)). This solution hinges a key observation: We search for a partition point in nums1 and nums2 such that there are an equal number of elements in the combined left and combined right partitions, and every element in the left is smaller or equal to every element in the right.
Lets look at this visually:
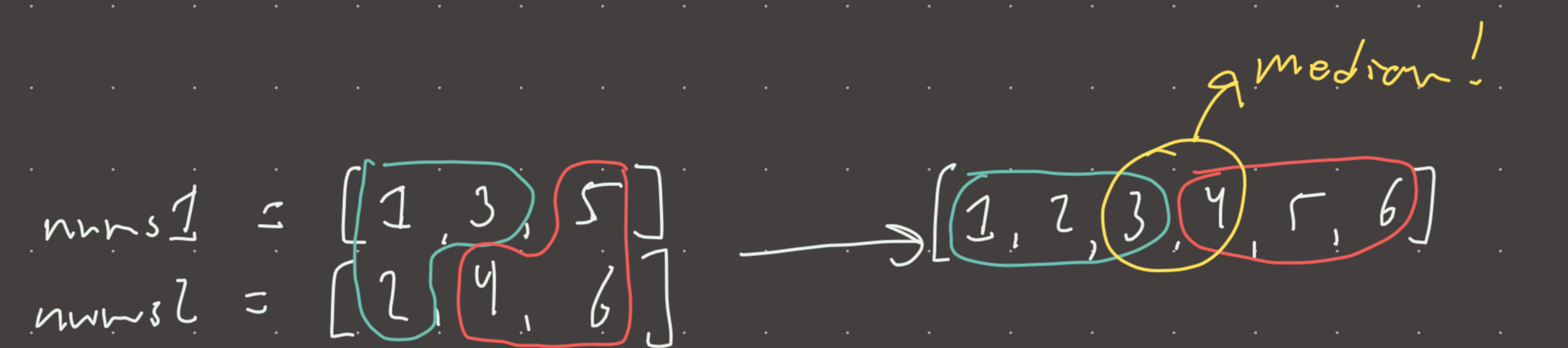
Take a look at nums1 and nums2. Every number in the left is smaller than every number in the right and there is an equal number of elements in both partitions! Basically, we can search for a partition point in nums1 and nums2 where these properties hold true! If this property is false, then we no longer consider the right half of nums1 as potential partition points. Why? Because moving the pointer further right would only increase the max value of the left partition, but we must find a partition point such that all elements in the left partition are smaller or equal to the right partition!
But how do we search for this partition across two arrays? Well, we only need to search through nums1, and the position in nums2 can be directly computed because the partition must have either (len(nums1)+len(nums2))//2 elements in the case that len(nums1)+len(nums2) is even, or (len(nums1)+len(nums2))//2 + 1 in the case of even.
The implementation is a mind-bender, but the main thing is to understand the concept above. Revisit this one a few times to nail the implementation because this seem to be a frequently asked question. I think the implementation is so funky because of the potential for out of bounds errors.
Implementation
def find_median(nums1, nums2):
if len(nums1) > len(nums2):
nums1, nums2 = nums2, nums1
odd = (len(nums1)+len(nums2)) % 2 == 1
l = 0
r = len(nums1)
while l <= r:
p1 = (l + r) // 2 #partition point in nums1
p2 = (len(nums1)+len(nums2)+1)//2 - p1 #partition point in nums2
left_max1 = nums1[p1-1] if p1 > 0 else float('-inf')
left_max2 = muns2[p2-1] if p2 > 0 else float('-inf')
right_min1 = nums1[p1] if p1 < len(nums1) else float('inf')
right_min2 = nums2[p2] if p2 < len(nums2) else float('inf')
right_min = min(right_min1, right_min2)
left_max = max(left_max1, left_max2)
if left_max <= right_min:
if odd:
return left_max
return (left_max + right_min)/2
elif left_max1 > right_min2:
r = p1 - 1
else:
l = p1 + 1
#time: o(log(n+m))
#memory: o(1)