Merge k sorted lists

Link: https://leetcode.com/problems/merge-k-sorted-lists/

Solution:

Topics: linked list, divide and conquer

Intuition
There are many ways to solve this problem, but by far the best way is the divide and conquer approach! With divide and conquer we can bring the complexity down to o(nlog(k))…or in other words, the total number of nodes n multiplied by the 2nd logarithm of the number of lists k. How?

In a perfectly balanced binary tree, the number of levels is log₂(k) + 1, where k is the number of nodes.

This is because log₂(k) gives you an estimate of the height of the tree, and the number of levels in the tree is one more than the height. So why is this useful?

Because we can essentially do the reverse of mergesort! Every node in our list of linked lists, is a leaf node in a binary tree whose root is the merged linked list!

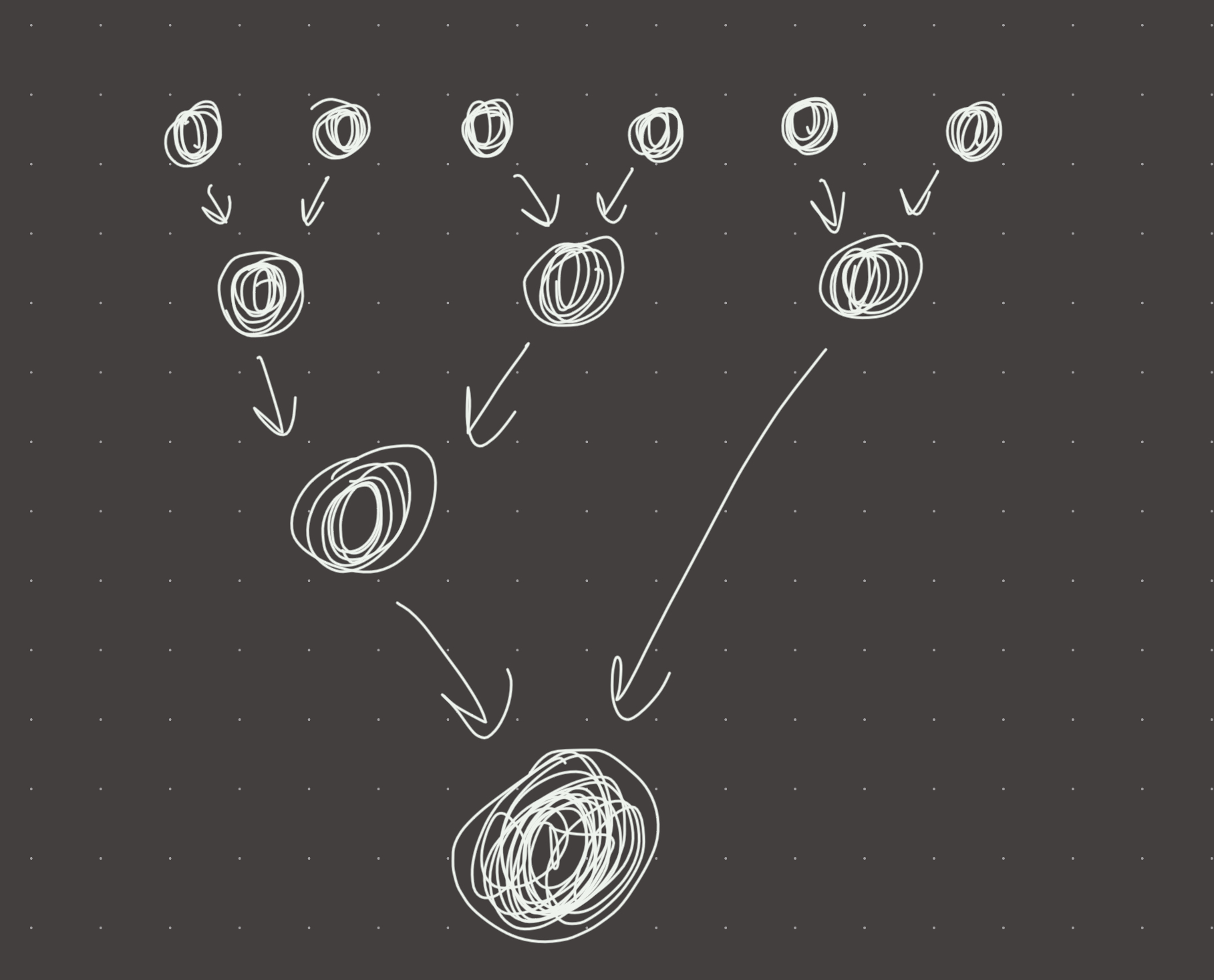
What this means more practically is that we can merge each pair of lists, and do until only one list remains! For example:

each star is a list

*   * *   * *   * *   *  start with 8 lists
 \ /   \ /   \ /   \ /
  *     *     *     *    merge each pair
   \   /       \   /
     *           *       merge each pair again
	   \        /
	     \    /
	        *            fully merged list

1. At each level, we spend o(n) time where n is the sum of total length of lists
2. The height of the tree is aprox. log(k). 

Thus the complitxy is o(nlogk)

Implementation

def merge_k_lists(lists):
	def merge(list1, list2):
		head = ListNode(-1)
		tail = head
		while list1 and list2:
			if list1.val < list2.val:
				tail.next = list1
				list1 = list1.next
			else:
				tail.next = list2
				list2 = list2.next
			tail = tail.next
		if list1:
			tail.next = list1
		if list2:
			tail.next = list2
		return head.next
 
	lists = deque(lists)  #deque not strictly required,						 
	while len(lists) > 1: #but I like the simplicity
		lists.append(merge(lists.popleft(), lists.popleft()))
	return lists[0] if lists else None
			
#time: o(nlogk)
#memory: o(1) ...ok the deque will add something but its worth it IMO

Mnemonic
You have 10 balls of dough. You must combine them all into 1 ball but you can only work with 2 balls at a time. You want to do this with the least effort possible. In other words, the “snow ball” technique is not your friend because you would be hauling around an increasingly heavy ball of dough…especially as you combine the last parts.

The correct strategy is to combine each pair of balls until only one ball is remaining. This way, the mass is more evenly distributed at each operation.

Visual

Review 1
This is very interesting. I found the heap approach almost instantly and in fact it’s the same time complexity as the divide and conquer solution, but worse memory. Cool to have found an approach that I had not considered previously! Progress! I like the heap solution better, but divide and conquer is technically better although not the first thing that would come to mind (probably).

review