Link: https://leetcode.com/problems/minimum-add-to-make-parentheses-valid/
Solution:
Topics: stack
Intuition
This is a nice little problem, not because of difficulty but more as an example for the clean implementation of various stack problems.
The key intuition here is understanding what makes a string invalid. It’s one of two conditions:
1. if there is nothing to pop off the stack: ))))
2. if the stack is not empty at the end of the algo ((((
Armed with these key insights, we can start to understand how to build a result. If condition 1, add to the result. Condition 2 is just the length of the stack at the end of the algorithm…add this to the result.
The constant space solution is kind of cute so I’ll implement it that way. I am essentially simulating a stack with a count.
Implementation
def min_len_par(s):
res = 0
count_stack = 0
for char in s:
if char == '(':
count_stack += 1
else:
count_stack -= 1
if count_stack == -1:
res += 1
count_stack += 1 #make sure to rebalance the stack
return res + count_stack
#time: o(n)
#memory: o(1)Mnemonic
We have a very demanding restaurant owner. The waiters must bring the customer exactly as much water as they can drink and exactly when they need it. If the cup is ever empty, or if water remains in the cup after the customer has paid their bill, the waiter is fired.
Visual
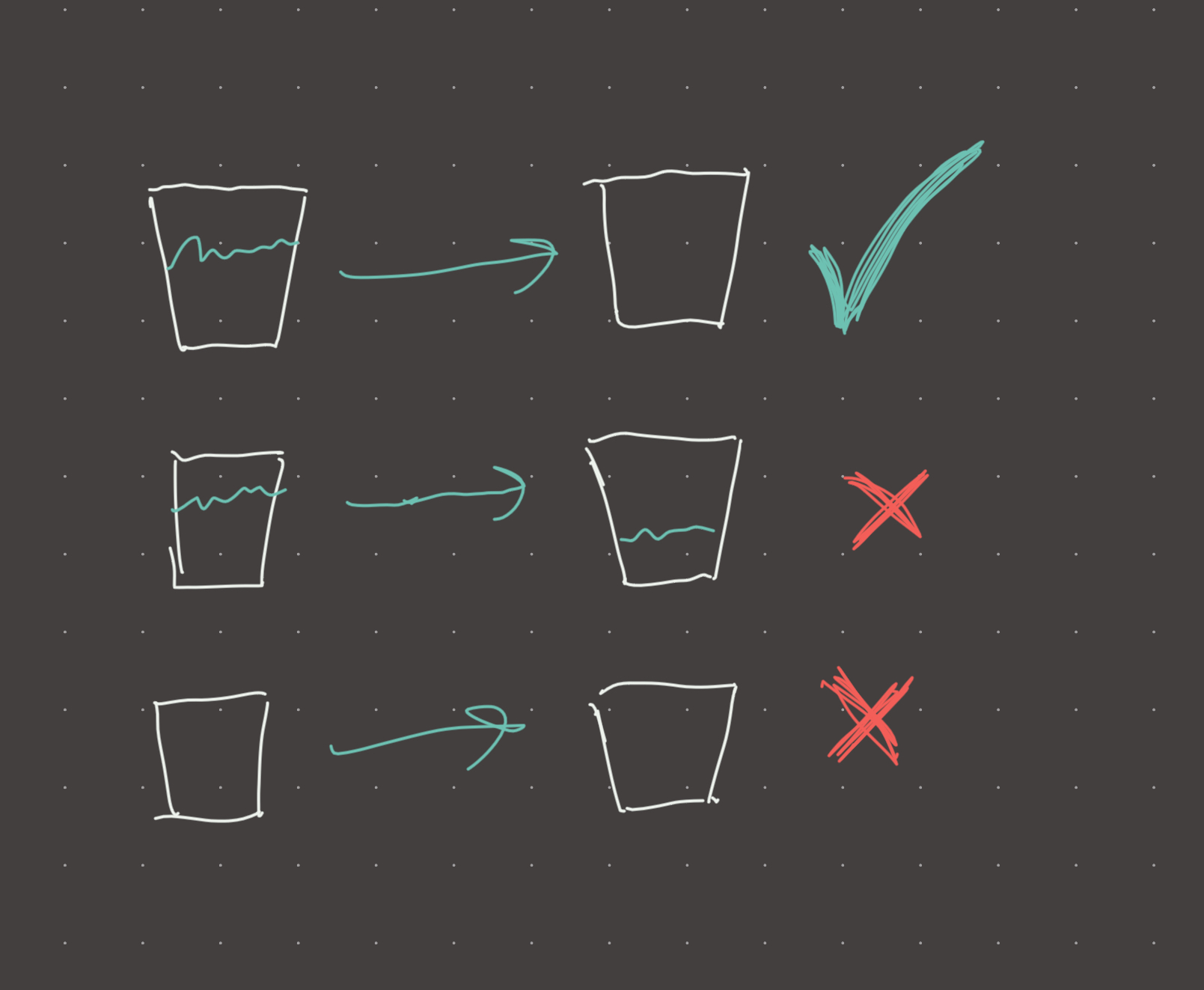
Review 1
Struggled with this one, but I had the right idea. Firstly the constraints threw me off. They were so generous that I thought the solution might be non-linear. Finally decided to go for a linear solution and pretty much used the same solution as in Longest valid parentheses…except I made a key oversight. In Longest valid parentheses we are looking for a single contiguous valid parentheses, whereas here we want the the length of ALL valid parentheses…so a valid subsequence. The length of s minus the length of the valid subsequence is the answer.
I think the solution above is a bit confusing. IMO it’s more elegant to count valid pairs rather than this whole rebalancing business. I’m tagging this hard because my thought process was erratic for this one even though I solved it very fast.
Implementation (valid pairs)
def min_valid(s):
stack = 0
valid_pairs = 0
for i, char in enumerate(s):
if char == ')':
stack -= 1
if stack == -1:
stack = 0
else:
valid_pairs += 2
else:
stack += 1
return len(s) - valid_pairs
Review 2