Link: https://leetcode.com/problems/minimum-cost-for-tickets/
Solution:
Topics: DP, binary search
Intuition
This should be easily recognizable as a DP problem, why? Because there are many combinations of tickets, and only a small subset (possibly only one) results in minimum cost. So we can explore the combinatorial tree with post-order DFS and prune the tree by choosing only the min for each branch (and then caching the result).
Binary search can also be used to speed up the algorithm (only slightly with the problem constraint of len(days) <= 365).
Implementation
def min_cost(days, costs):
def bs(i, travel_days):
target_day = days[i] + travel_days
return bisect_left(days, target_day)
@cache
def dfs(i):
if i == len(days):
return 0
one = costs[0] + dfs(i+1)
seven = costs[1] + dfs(bs(i, 7))
thirty = costs[2] + bfs(bs(i, 30))
return min(one, seven, thirty)
return dfs(0)
#time: o(nlogn) n = len(days)
#memory: o(n)Mnemonic
You are traveling. Clone yourself 3 times and by 3 different train tickets (1, 7, 30). Jump to the nearest non-traveled day. Only the clone with min-cost remains.
Visual
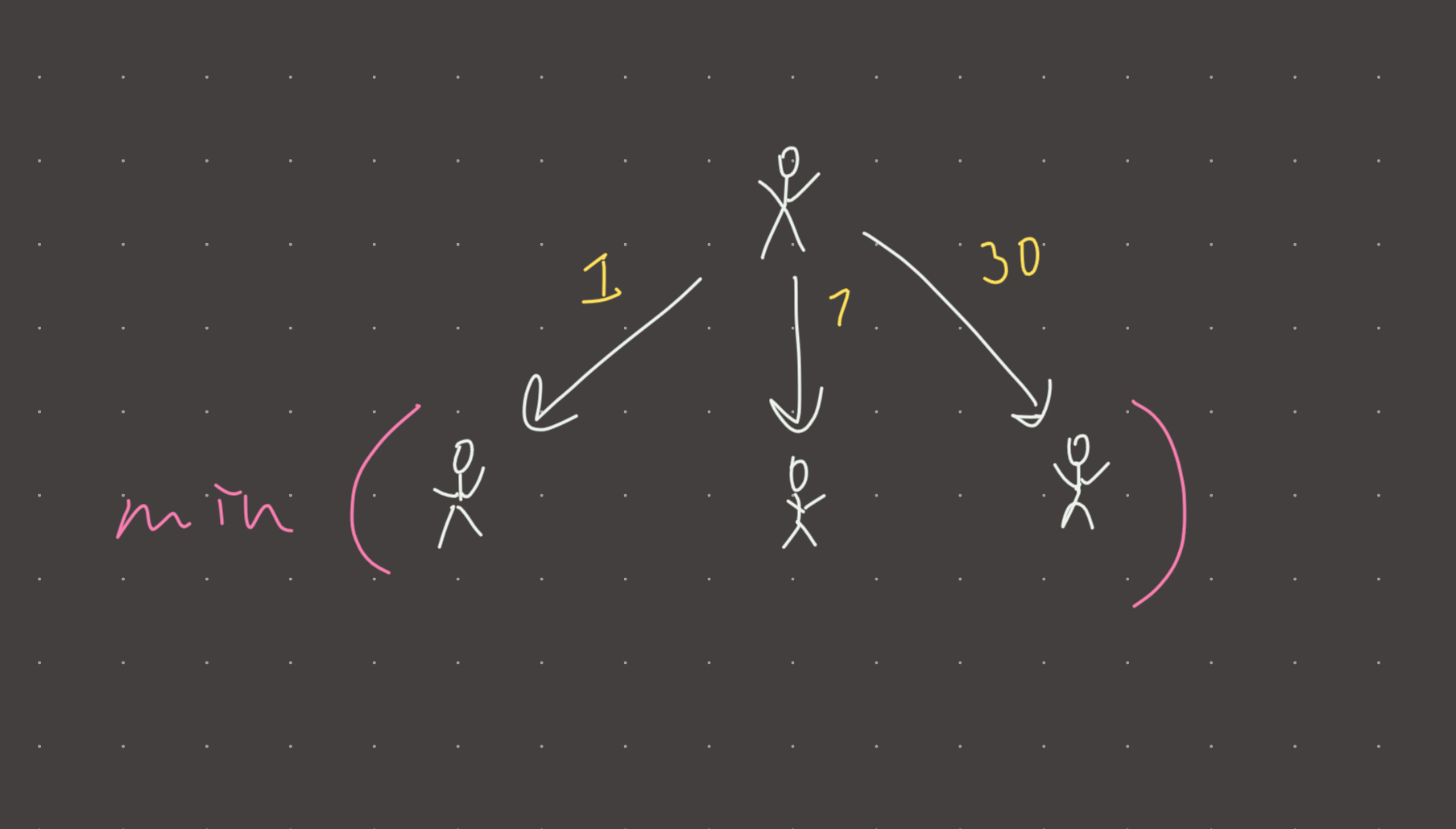
Review 1
Very similar problem to Maximum profit in job scheduling! Basically, we must find the next position to optimize the DP tree.