Link: https://leetcode.com/problems/minimum-number-of-coins-to-be-added/
same problem: https://leetcode.com/problems/patching-array/
Solution:
Topics: math
Intuition
Extremely challenging problem if nothing similar has been seen before. I had to look at a solution…and even after seeing some solutions it took me a while to understand why the algorithm even works. Its kind of simple once you “get it”, but very tricky to get there nonetheless.
The key here is mathematical induction. Lets start by understanding how to even create an array where all numbers between 1-n can be formed:
[0,1] start here.... 1 and 0 can be formed.
[0,1,2] add a 2... now 2 can be formed
BUT ALSO 3 CAN BE FORMED!!!
Think about it, before appending the 2, we know that 0 and 1 can be formed...so the new "maximum" number that can be formed is simply the previous maximum (1) + 2! Thus the new maximum that can be formed is 3
Lets keep going...we can already form 3 so what will be the next number? 4!
[0,1,2,4] 4, 5, 6, 7 can be formed!...or new_max = apended_num + old_max
Lets keep going...append 8!
[0,1,2,4,8] new max is 8+7 (15)!
But what about the gaps? In the second last iteration of our algorithm, we jumped from a max of 3 to a max of 7…why is it guaranteed that 5 and 6 can also be formed? It is guaranteed because previously we proved that 1 and 2 can be formed, and since we are adding 4, it can be added to 1 and 2 to form 5 and 6.
Basically, by following the algorithm, we keep a “bank” of numbers that are guaranteed to be formed, and when we append to the array, we are also guaranteed to form every number between the range old_max to new_max.
With that out of the way, lets look at the problem. We are given an array that we can use to “help” with the forming. The first thing to notice about our algorithm is that the numbers added to the array are in increasing order…so if we are to use coins, they must be sorted as well.
With the sorting complete, lets try to understand how to use the coins given to us. Basically, if the current coin is smaller or equal to the current_max+1, we can use it to extend our range with new_max = old_max + coin[i]. Why is this the case?
This is the case because we can never extend beyond current_max + 1 and still guarantee no gaps! For example:
[0,1,2] 3 is the current_max that can be formed...the next number should be current_max + 1 (4)....but what if we added 5 instead?
[0,1,2,5] invalid because 4 cannot be formed.
For current_max + 1 to be formed, it must exist ALONE because any number that exists before it, would by definition create a subset with current_max + 1 that would exceed the value of current_max + 1. The current_max is the cumulative sum of the array…there does not exist a subset inside the array that could form current_max+1 or greater because current_max already contains all elements…it is the limit.
Implementation
def min_coins(coins, target):
coins.sort()
res = 0
reachable = 0
i = 0
while reachable < target:
if i != len(coins) and reachable + 1 >= coins[i]:
reachable += coins[i]
i += 1
else:
reachable += reachable + 1
res += 1
return res
#time: o(nlogn)
#memory: o(1)Mnemonic
You have a very strange seed. Your task is to grow it into a plant until a certain weight has been reached…there is one nuance though. If you give the plant/seed more than exactly its own weight + 1ml of water, the plant will die. It just so happens that we already have some pre-filled jugs that you would like to use to water the plant. The only problem is, if we use some of these jugs too early, the amount of water will kill the plant. If we use these jugs too late, we will have to water more times than necessary.
If the water in a jug weighs less than or equal to the plant’s weight + 1ml…we can use the jug! Otherwise, go fill up plant_weight + 1ml of water and water the plant.
Visual
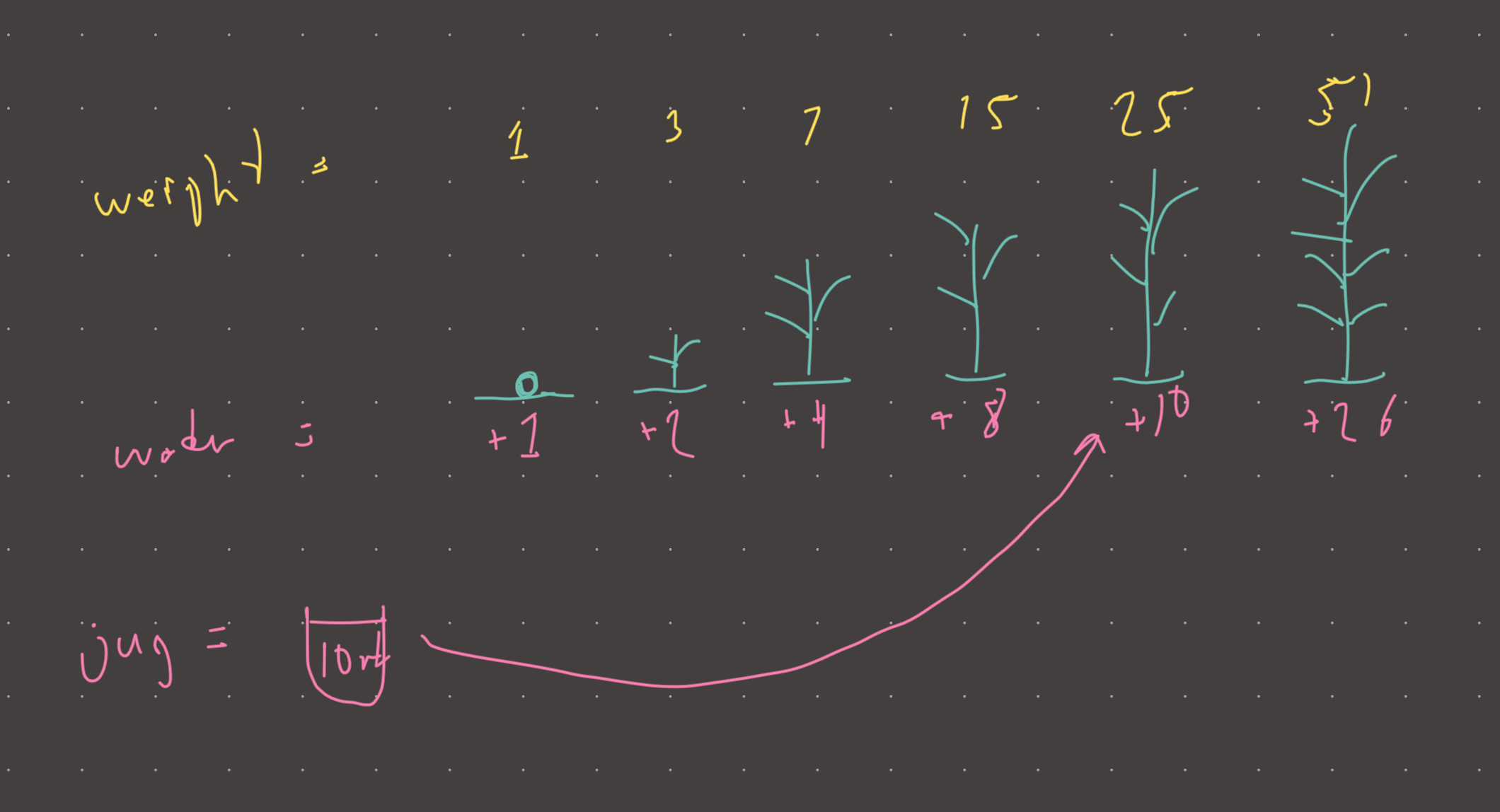
Review 1
Absurdly hard problem! I made a lot more headway on it than the first time though so I guess I should be happy about that. I understood the problem and even how to solve it but this one in particular is so particular about the implementation.
The key is doing two things:
- use a while loop and a pointer
ifor coins. - explicitly code the condition where we take the current coin, otherwise add a coin (and increment the result)
As a side note, understanding my mnemonic is more mind bending than the problem itself…