Link: https://leetcode.com/problems/minimum-operations-to-reduce-x-to-zero/
Solution:
Topics: sliding window, subarray
Intuition
This is an excellent example of what I call a “transformation” problem. Not transformation in the mathematical sense, rather a transformation of the problem statement into another one that is far more approachable but still gets you to the same result.
The problem is asking us to pop numbers from the left or right of nums until x can be made zero (with minimum pops). When you view the problem in those terms, techniques like 2-pointer come to mind…which don’t work because its impossible to make a locally optimal decision about which pointer gets moved.
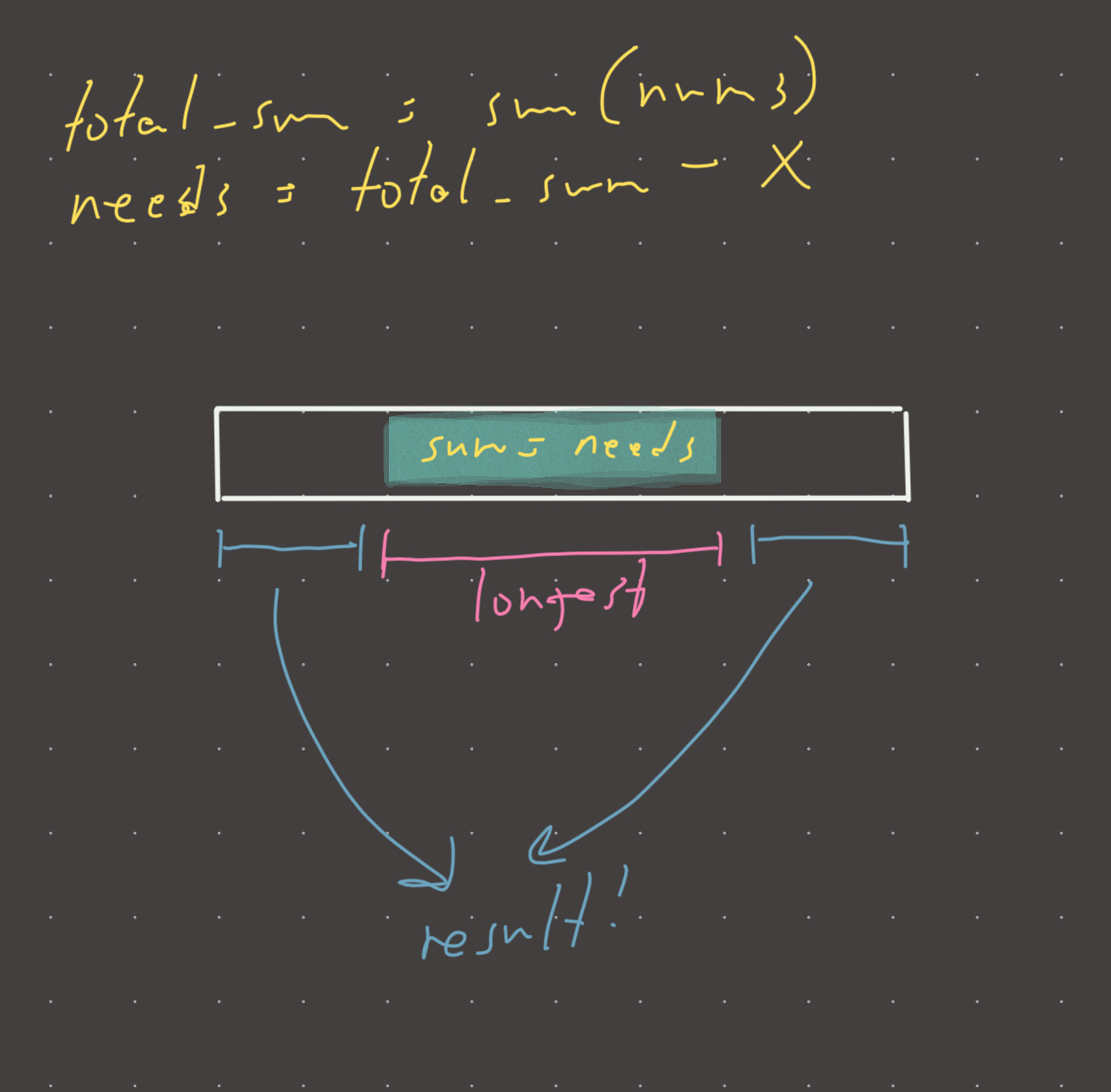
Instead of concerning ourselves with the left and right partitions of nums, we turn our focus to the contiguous middle partition connecting both sides! With this approach, we can simply find the longest such middle partition whose sum ensures that the sum of the left and right partitions amount to x. The sum to look for in our middle partition is trivial to derive:
needs = sum(nums) - x
Ergo, the result would be the total length of nums minus max_len_middle_partion (the number of elements in left and right partitions).
There are three notable edge cases. If x > sum(nums), its impossible; return -1. If x == sum(nums), return len(nums). The third edge case is a bit more subtle. There could be no way to sum up to needs even if sum(nums) is permissive so we take that into consideration when returning the result (for example there is no subarray in [1,3] that has a sum of 2).
Implementation
def min_operations(nums, x):
needs = sum(nums) - x
if needs < 0:
return -1
if needs == 0:
return len(nums)
max_len = 0
curr = 0
l = 0
for r in range(len(nums)):
curr += nums[r]
while curr > needs:
curr -= nums[l]
l += 1
if curr == needs:
max_len = max(max_len, r-l+1)
return len(nums) - max_len if max_len != 0 else -1
#time: o(n)
#memory: o(1)Visual
Review 1
I fell into the DP trap with this one. DP is a valid way to solve this problem but the complexity will be o(n*n) because we would need to keep two pointers l, r in the DFS cached function.
Upon further analysis, this problem wants us to find the smallest partitions on the left and/or right that sum up to x. Or in other words, the longest possible subarray in the middle (or starting at either or both sides) that sums to sum(nums)-x!
Spend a bit more time thinking about the problem rather than assume one approach is correct…especially if the first thing that comes to mind is DP.