Minimum replacements to sort the array

Link: https://leetcode.com/problems/minimum-replacements-to-sort-the-array/

Solution

DSA: subarray

Intuition
Iterating backwards, we only need to consider cases where nums[i] > nums[i+1]. In this case, we must replace nums[i] with a subarray that sums to nums[i], and with the greatest possible value as its first element.

For example:

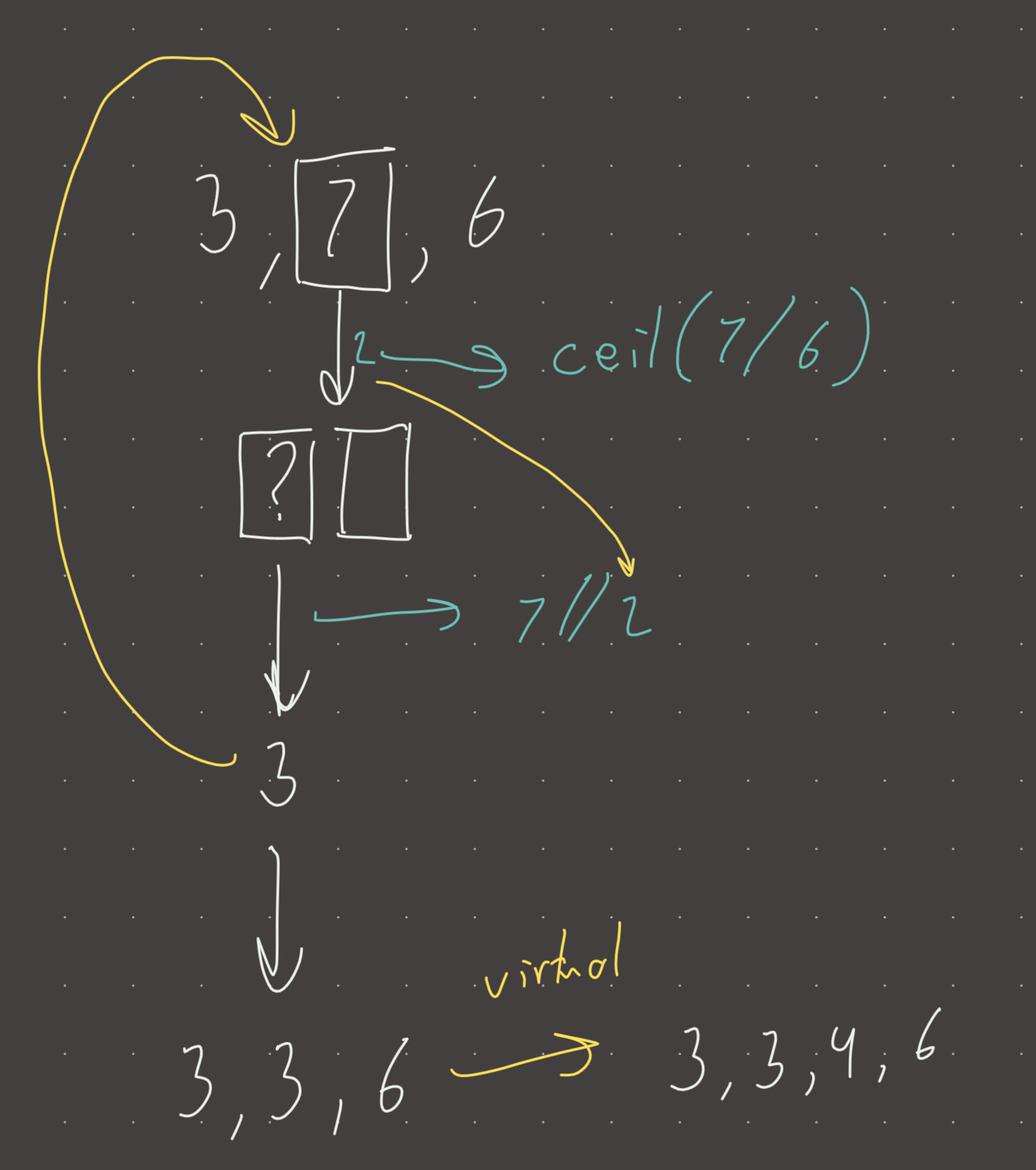
nums = [3, 7, 6] #we can see that 7 must be split, but how?

#if we split 7 into [1, 6], we can move on, but we have 1 as the last element
#which means that we must also split 3 into [1, 1, 1] increasing the splits
#optimally, we would split 7 into [3, 4]...no further splitting required 

So how do we split a number optimally? There is actually a trick. First we must determine the minimum length of the new subarray such that the last element is smaller or equal to nums[i+1].
Here is how:

length = math.ceil(nums[i]/nums[i+1]) # ceil(7/6) in our example

How does this work? Well, when we do 7/6, we are asking: how many times does 7 fit inside 6? The answer is 1.17, but since we need a LENGTH, the remainder gets its own spot! Which means that we round up when there is a remainder! So 1.17 becomes 2.

The length of 2 gives us the minimum length of the split such that no element is greater than 6, but we still need the optimal first value in that subarray. We determined earlier that [3,4] is the optimal split…we know the length, but now we need a way to get 3! Why? Because 3 will replace 7 in the array, in case further splitting is required.

Here is how:

first_num = nums[i]//length # 7 // 2 in our case

Why does this work? Because 7/2 is 3.5 which would split 7 evenly across the length, but splitting into floating point numbers is not allowed, even though its more optimal, so we have to settle with rounding down. Note that we cannot round up because [4,3] is decreasing.

The number of splits is length - 1 because the first split counts as one even though the subarray length is 2.

Implementation

def min_replacements(nums):
	res = 0
	for i in range(len(nums)-2, -1, -1):
		if nums[i] > nums[i+1]:
			length = ceil(nums[i]/nums[i+1])
			first_num = nums[i] // length
			nums[i] = first_num
			res += length - 1
	return res

Visual

Review 1
I knew this problem had a greedy solution but I forgot the math trick. It is actually very clever. Not too different from Find missing observations.

1. The length of the subarray produced by splitting is ceil(nums[i] / nums[i+1]). Its rounded up because the remainder takes a full spot.
2. The leftmost number is nums[i+1] // length.
3. The number of operations is length - 1 because a length of two is created by one operation.

review