Link: https://leetcode.com/problems/next-permutation/
Solution:
Topics: sorted order, permutation
Intuition
The problem statement here is very unclear in my opinion. The use of the word “lexicographical” made me consider the lexicographical value of the number if it was concatenated and converted into a string.
For example:
'100' is lexicographically smaller than '11'
Although the above interpretation is what is typically referred to when the term “lexicographic” is applied to a number, this is NOT the case here. It’s also not the case that “lexicographically greater” is referring to a permutation of which the concatenated value is “just” greater than the concatenated value of the current permutation.
For example:
[8,11,3] ----> the 'concatenated' value is 8113
The "just" greater interpretation would yield the following:
[8,3,11] ----> the 'concatenated' value is 8311
8311 > 8113, so is this the "next permutation"?
NO! It's actually [11, 3, 8]
So what actually is the next permutation if its not related to the concatenated string or concatenated value? The key here is to think of each number in the permutation as a single entity in an pseudo-alphabet. The lowest value would be analogous to ‘A’ and the highest value would be analogous to ‘Z’.
The magnitude of each number in the permutation refers to it’s position in this pseudo-alphabet.
Lets look at our example again:
[8,11,3] becomes ---> [b, c, a] (we dont need more letters)
So if we consider [8,3,11] from the previous example, we get:
[b, a, c]
We can see tha 'bac' is lexographically SMALLER than 'bca'!
The correct answer is [11,3,8] ---> [c, a, b]
And indeed 'cab' is lexographically GREATER than 'bca'
So building off this example, if we treat each element as it’s own entity and lexicographical position, we just need the make the smallest increase that we can. How?
Consider:
'abcd'
There are many ways to increase the lexicographical value of 'abcd', but the smallest change we can make is by swapping 'c' and 'd'
Thus the next permutation is 'abdc'.
We want to alter the righmost elements that we can, because this guarantees the least amount of lexicographical change. We can of course swap 'a' and 'd' to make 'dbca', but the lexcigographical value is increased much more than needed.
More complex example:
'abcdgfe'
Starting from the right, we find 'fe'. Can we swap them? We cannot because the lexicographical value would DECREASE to make 'abcdgef', and we don't want the previous permutation, but the next one.
Now starting from the 'g', we find 'f' and 'e' as potential swap candidates, but they both come before 'g' lexicographically so these swaps would also DECREASE the lexicographical value.
Starting at 'd', we find that all values to the right (gfe) are valid swaps because they come after 'd' in the alphabet and would thus INCREASE the lexicographical value. But which to choose? Naturally, we must choose 'e' because we want the smallest increase possible and 'e' is closest to 'd' among all characters in the right partition (gfe).
Swapping 'd' and 'e' creates 'abcegfd'. Is this the next permutation? No!
'abcegfd' is not the next permutation, but we are close. Lets consider the right partition [g,f,d]. Since we already increased the lexicographical value, by swapping 'd' and 'e', we must also modify the right partition [g,f,d] to be of the SMALLEST lexicographical value possible because otherwise the overall lexicographical value of [e,g,f,d] is needlessly high and we want the MINIMUM increment.
The smallest lexicographical permutation of 'gfd' is 'dfg' so our next permutation is 'abcedfg'.
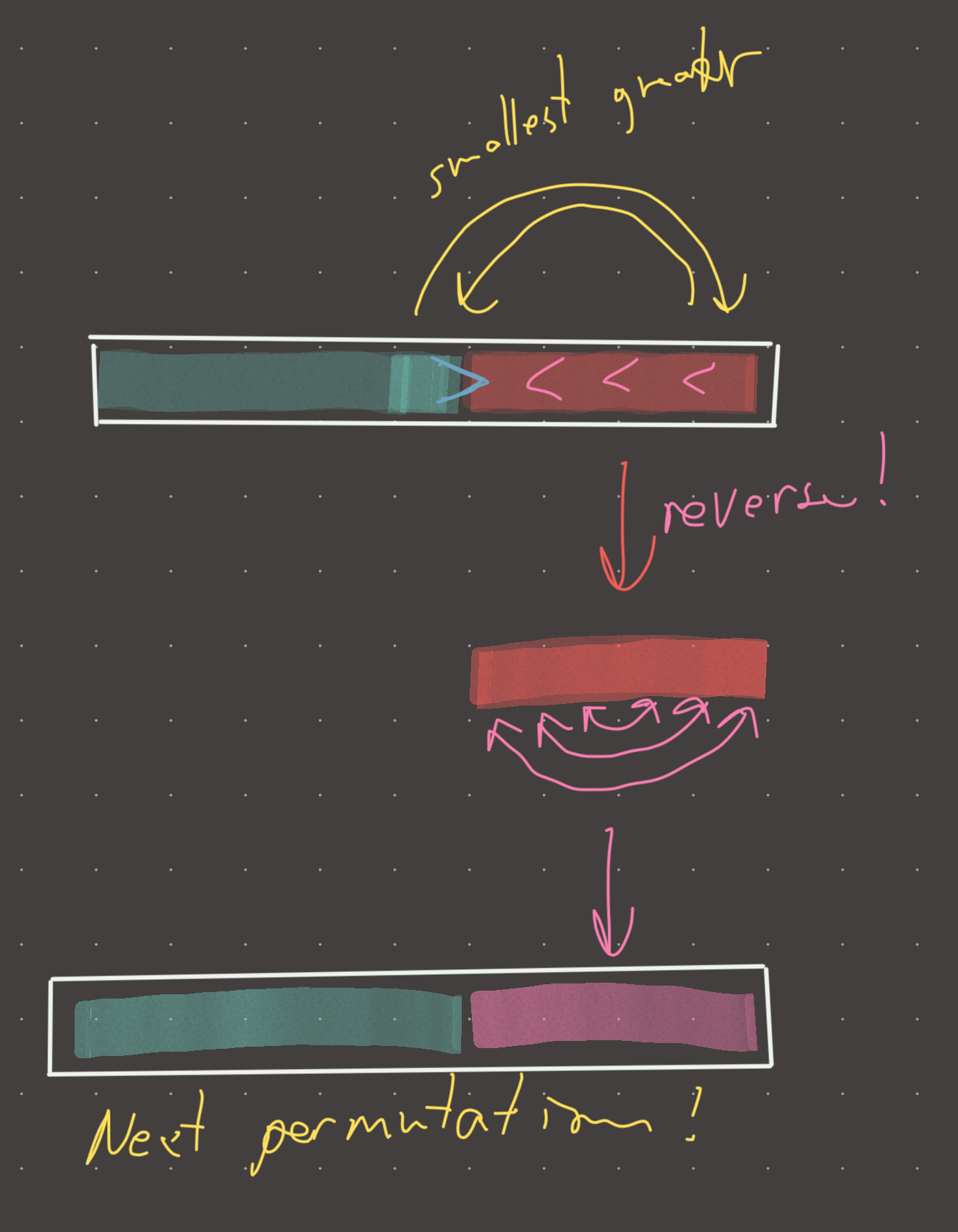
How do we find the smallest permutation of the right partition after the swap? Well, we can just sort it in increasing order, or we can simply reverse it in-place! Why does this work?
Reversing works because the right partition is guaranteed to be in DECREASING order! This is because if we are checking for greater rightmost values to swap with, if a valid swap is not found, the partition is by definition DECREASING!
In our original example 'abcdgfe', the first valid swaps were found for 'd', but notice that the partition after 'd' (gfe), is in decreasing order.
This is also a good explanation
Implementation
def next_permutation(nums):
def reverse(l):
r = len(nums)-1
while l < r:
nums[l], nums[r] = nums[r], nums[l]
l += 1
r -= 1
for i in range(len(nums)-2, -1, -1):
if nums[i] >= nums[i+1]:
continue #partition is decreasing, no swaps possible
for j in range(len(nums)-1, i, -1):
if nums[j] > nums[i]:
nums[i], nums[j] = nums[j], nums[i]
reverse(i+1)
return
reverse(0)
#time: o(n) #not n^2 because of early exit condition (nums[i] <= nums[i+1])
#memory: o(1)Visual
Review 1
Tough problem! I correctly interpreted the problem and got most of the way to a solution but I made one key oversight.
Basically, when we swap two numbers, three things are possible:
- Increase in lexicographical value
[1, 2] ---> [2, 1] - Decrease in lexicographical value
[2, 1] ---> [1, 2] - No change
[1, 1] ---> [1, 1]
We are looking for the next greater permutation so we are only allowed to increase the lexicographical value. What this means is that when nums[i] < nums[i+1], there is a valid swap available to us. So do we swap nums[i] and nums[i+1]? NOT NECESSARILY! Why?
Consider the following:
nums = [1, 3, 2]
We can see that 1 < 3....and swapping them would yield [3, 1, 2] which is indeed lexicographically greater.
But this is incorrect because we should swap with the 2 to make [2, 1, 3] !
The later is lexicographically smaller than the former!
Also notice that 1, 3 swapped places after 1, 2 swapped places. This is due to the fact that everything past the 2 must be sorted in decreasing order. We already know that that partition is decreasing, so reversing it will make it sorted in increasing order!
So does this mean we always swap nums[i] with nums[-1]? NO!
Why?
Consider the case nums = [2, 3, 1]
We can see that the swapping 2 and 1 is illegal because that results in a smaller permutation!
Essentially, we cannot know in advance what the leftmost greater element is in the right partition unless we acually look. So the solution is to iterate backwards from len(nums)-1, and the first number that is greater than nums[i] is swapped with nums[i]. You could also do binary search because the right partition is guaranteed to be sorted in decreasing order.
In the case that no swapping condition is met, we simply reverse the array as we are wrapping back to the smallest possible permutation.