Number of provinces

Link: https://leetcode.com/problems/number-of-provinces/

Solution:

Topics: DFS, union find

Intuition
This is a kind of annoying variation on the connected components class of problems. The reason why it’s annoying is because the graph is given in a strange form which complicates the graph traversal. On first glance one could think think that the connected components are adjacently connected 1’s but this is not the case.

Each node must be connected to itself…which doesn’t really make sense but this is how the graph is modelled.

For example:

    connected to 3 
        /        |
[1, 0, 1]        |
[0, 1, 0]        | this is a valid connection,
[1, 0, 1]        | the traversal must jump from 
  \              | city 1 to city 3
   connected to 1

There is also a union find solution, which is extremely efficient for relationship graphs…it’s also the only efficient way to find connected components in dynamic graphs (updating relationships). Not a perfect use case here because our graph is static but none the less an interesting approach.

Implementation (DFS)

def number_of_prov(isConnected):
	def dfs(city):
		if city in visited:
			return False
		visited.add(city)
		for i in range(len(isConnected)):
			if i == city:
				continue
			if isConnected[city][i] == 1:
				dfs(i)
		return True
		
	visited = set()
	provs = 0
	for i in range(len(isConnected)):
		if dfs(i):
			provs += 1
	return provs
		
#time: o(n**n) for n*n matrix
#memory: o(n**n) stack space

Implementation (union find)

class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))
        self.count = n
 
    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
 
    def union(self, x, y):
        root_x, root_y = self.find(x), self.find(y)
        if root_x != root_y:
            self.parent[root_x] = root_y
            self.count -= 1
 
class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        n = len(isConnected)
        uf = UnionFind(n)
 
        for i in range(n):
            for j in range(i + 1, n):
                if isConnected[i][j] == 1:
                    uf.union(i, j)
 
        return uf.count

Visual

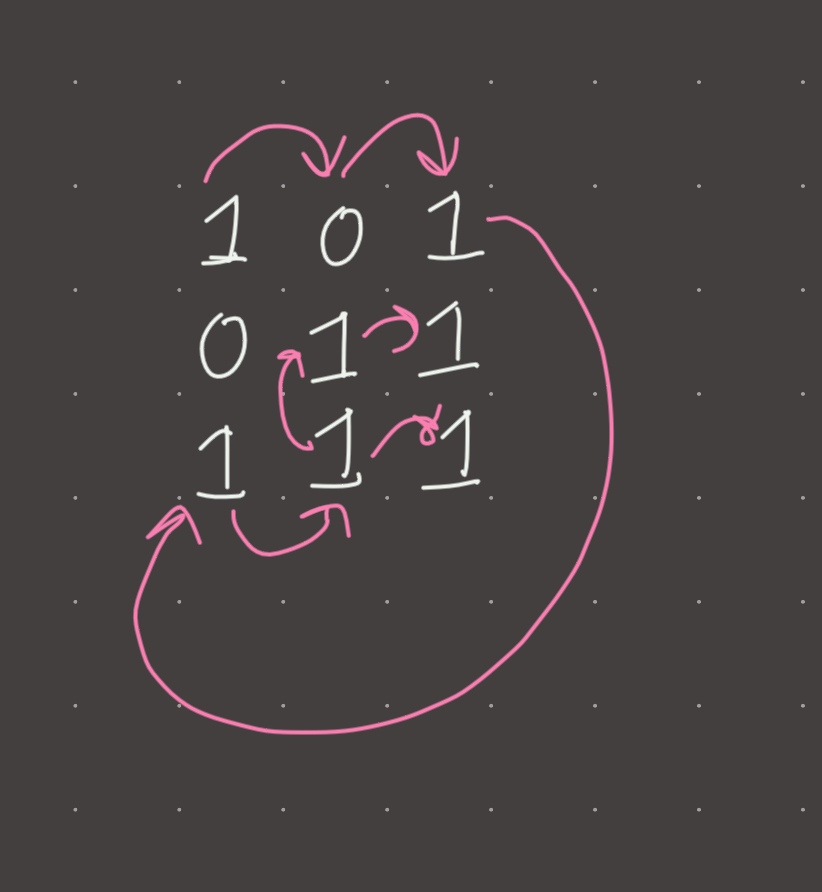
Review 1
The easiest solution here is to build an adjacency list and count components. The slightly better solution is to traverse the matrix as-is! This is a more subtle solution but eliminates the need for an adjacency list. The even more subtle solution is to use union find.

Its a tricky one because traversing the matrix is not straight forward.

review
hard