Link: https://leetcode.com/problems/painting-the-walls/
Solution:
DSA: DP, DFS, subsequence
Intuition
This seems like a heap problem, but its not. The reason why it’s not is because there is not an optimal way to use the paid painter and the free painter. It seems like you can use a min_heap for the paid painter and max_heap for the paid painter…but there are edge cases where this does no work. There are cases where choosing a higher cost/time wall is more optimal for the paid painter because its also about making sure the paid painter is working whenever the paid painter is!
For example:
cost = [1, 2, 3, 4]
time = [2, 1, 2, 1]
ratio = [0.5, 2, 1.5, 4]
#if we put ratio into a min_heap and max_heap we get the following order
min_heap = [0.5, 1.5, 2, 4]
max_heap = [4, 2, 1.5, 0.5]
#if we follow this strategy, the walls corresponding to 0.5 and 1.5 get painted by the paid painter which would cost 4. But the real min cost is 3! How?
#if we give the paid painter index 0 and 1, the total cost is 3 and the duration is 3 days, which means that the paid painter can paint index 2 and 3 in that time (needs only 2 days for that)!
#in the min/max heap strategy, our paid painter would be occupied for 4 days, and while that has a more favorable cost/time ratio, the total cost at the end would be greater because we only had to work for 2 days in order to activate the paid painter to finish the rest of the walls!So now that the heap strategy has been invalidated, lets talk about how to actually solve this problem.
It boils down to this insight: for every wall that we assign to the paid painter, the free painter can paint time[i] walls. We don’t actually care which walls the free painter paints, because we can choose a min subsequence of walls, such that the number of walls painted is greater or equal to the total number of walls.
For example:
#(cost, time) for simplicity
walls = [(1, 2), (2, 1), (3, 2), (4, 1)]
#lets chose subsequence [(1,2)]...the total walls painted would be 3 (the free painter can paint 1 wall for each unit of time (2 in this case), and the paid painter paints that single wall (1))
#the cost is only 1, but we cant take it becaue wee need to paint at least 4 walls, but we can only paint 3.
#lets choose subsequence [(1, 2), (2, 1)]...the total walls painted would be 5, so its possible to complete the job, and the total cost is 3.
#lets choose subsequence [(1, 2),(3, 2)]..the total walls painted would be 6, which completes the job but the cost is 4 which is greater than the previous subsequence and less optimal.
#FOR SUBESQUENCES USE DP!!!Implementation
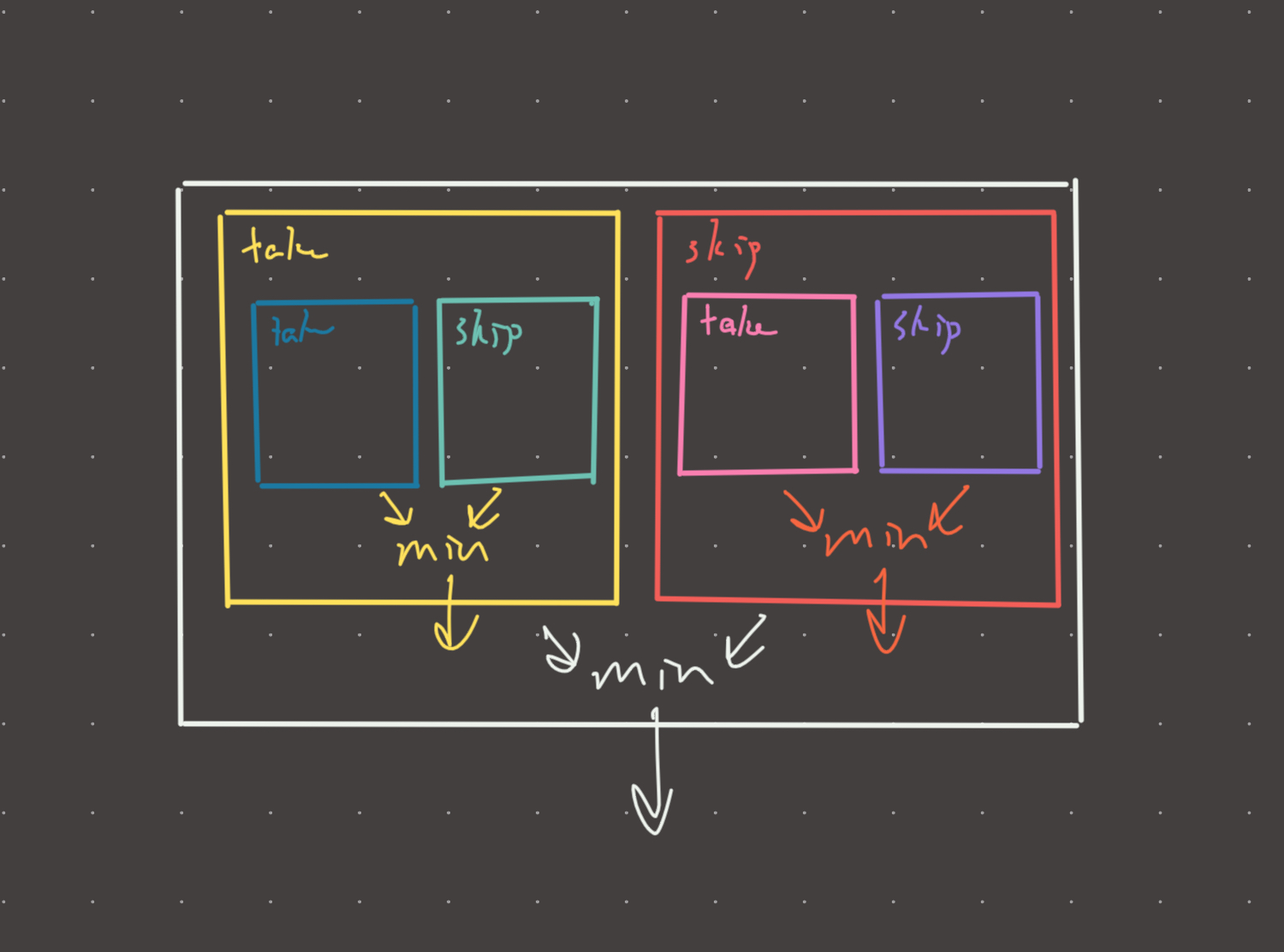
def painting_walls(cost, time):
n = len(cost)
@cache
def dfs(i, walls_painted):
if walls_painted >= n:
return 0
if i == n:
return float('inf')
take = cost[i] + dfs(i+1, walls_painted + 1 + time[i])
skip = dfs(i+1, walls_painted)
return min(take, skip)
return dfs(0, 0)
Visual
Review 1
I misread the problem and thought we were solving for minimum time and found a DP solution there. The actual problem here is requires solving for min cost! I comes down to the following:
We can either incur the cost of painting the wall and then recruit our free painter, or we can not do anything with the hopes that the free painter will get to that wall at some point when we do chose to incur cost.
For example:
cost = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
time = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 100]
In the above case, we can see that it make sense to wait until the last wall to incur the cost, because that last wall takes 100 units of time which means that our free painter can paint 100 walls. We only need 12 walls painted, so since 101 (including the wall painted by our paid painter) is greater than 12, all walls have been painted at a cost of 1.
Essentially we are looking for the subsequence that reaches num_walls the cheapest. The walls don't have to be painted in any particular order so subsequence works here.