Link: https://leetcode.com/problems/race-car/
Solution:
Topics: BFS
Intuition
This is a very interesting problem! I recognized right away that this was either a BFS problem or greedy…the second was eliminated as a possibility early on though. Why is this BFS? Because this is a search problem and we are looking for the shortest path to the target. The branching factor is also low, so BFS is suitable (each parent has at most 2 children in the permutation tree).
There are only two paths we can choose…we can either continue accelerating or reverse. Of course we could explore all possibilities indiscriminately to find the shortest path, but this would result in MLE so we have to find some optimizations.
The key insight here is choosing the right time to reverse. Acceleration is the default mode and that branch should always be explored (ok, within reason but for these constraints we can assume this to be the case). So how do we chose when to explore the reversing branch?
If the curr_pos + speed > target and speed > 0, then we should explore the reverse branch. This condition is equivalent to “overshooting” the target, so we should consider the possibility that its better to reverse twice to slow down! But is it always better to slow down?
No! It may be the case that we should overshoot and then reverse. Or it may be the case that we should oscillate around the target before converging…thats why we always explore the “accelerate” branch. Technically this does result in a branch that approaches infinity, and just as many spurious “reverse” branches…we could come up with some conditions to kill these branches but for the constraints of the problem target <= 10**4, there is no need.
Implementation
def race_car(target):
queue = deque([(0, 1, 0)])
while queue:
pos, speed, moves = queue.popleft()
if pos == target:
return moves
next_p = pos + speed
if (next_p > target and speed > 0) or (next_p < target and speed < 0):
queue.append((pos, (-speed)/abs(speed), moves + 1))
queue.append((pos+speed, speed * 2, moves + 1))
#time: o(log(target))
#memory: o(log(target))Mnemonic
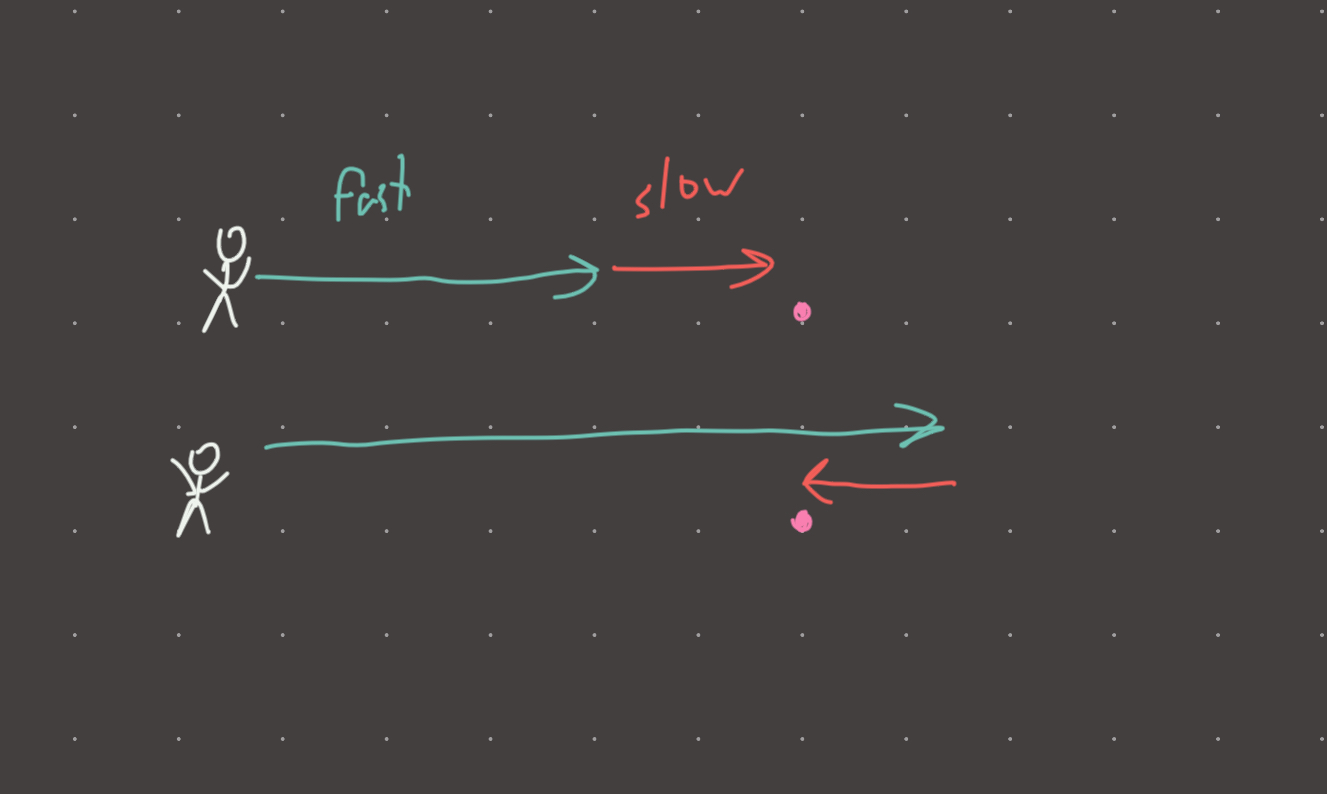
There is a marble some distance away from you. Your task is to pick up the marble as quickly as possible. Unfortunately you can’t grab the marble while running fast, so you need to slow down and kneel over to pick it up. Or you can run past the marble and then back up slowly to pick it up. You don’t know which is faster, so you clone yourself and try both options.
Visual
Review 1
I was pretty disappointed at my performance in this problem. I think I was trying to solve it from memory and got lost trying to find a greedy solution. What’s funny is that BFS was the first thing that came to mind and my faulty memory convinced me to discard it.
It should be clear why there is no greedy solution: its impossible to know if we should reverse or accelerate in the case that acceleration would overshoot the target. Only in the overshoot case do we explore the reverse branch, as it is always more optimal to accelerate otherwise.