Remove colored pieces if both neighbors are the same color

Link: https://leetcode.com/problems/remove-colored-pieces-if-both-neighbors-are-the-same-color/

Solution:

Topics: greedy

Intuition
This becomes a very easy problem when we realize that how Alice plays can never affect how Bob plays and vice versa…or in other words, moves by one player can never open up or limit the moves of another player. Why?

BBBAAABBB

AAA can only be reduced to AA, so contiguous subarrays of either A or B will always remain as isolated islands.

With that insight out of the way, The problem just becomes: are there more instances of AAA or BBB? Why?

Lets look at a base case:

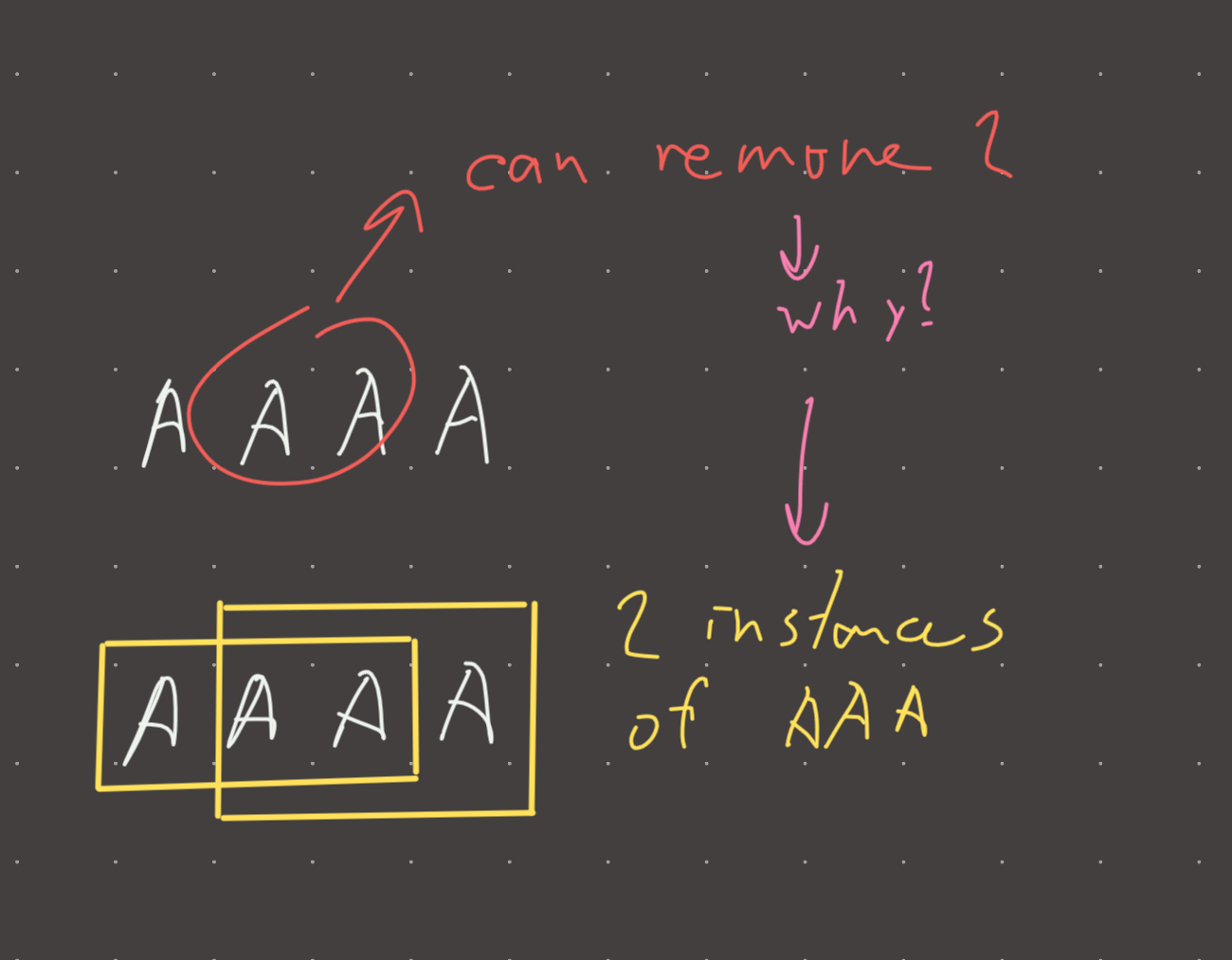
AAA - 1 instance of AAA, this is one move
AAAA - 2 instances of AAA, two moves
AAAAA - 3 instances of AAA, three moves

So we count the number of moves possible for both Alice and Bob, if Alice can make more moves than Bob, Alice wins. Otherwise Bob wins. Or alternatively we can keep a score. If the score ends negative or zero, Bob has won.

Implementation

def colored_game(colors):
	score = 0
	for i in range(2, len(colors)):
		if colors[i] == colors[i-1] and colors[i] == colors[i-2]:
			if colors[i] == 'A':
				score += 1
			else:
				score -= 1
	return score > 0
	
#time: o(n)
#memory: o(1)

Visual

Review 1
Fun greedy problem. My article here is quite good. Solved this one very fast…remember that both scores can be folded into a single “balance”. If we increment for Alice and decrement for Bob, the result becomes the boolean score > 0.

review