Restore ip addresses

Link: https://leetcode.com/problems/restore-ip-addresses/

Solution:

Topics: DFS

Intuition
This is a nice little recursion problem. It should be clear that recursion should be used here because of the result is built up in a decision tree.

For example:

s = '11111'
                      ''
                    /   \
                  1.     11.
              /   \       /   \
          1.1.  1.11.    11.1.  11.11.
       ...

After this, it’s simply a matter of setting up the recursion correctly to ensure that the leaf nodes are valid ip’s. The base case is if all digits in s have been used and if the length of the built string is equal to the length of s plus 3 (three dots):

if i == len(s) and len(curr) == len(s) + 3:
	res.append(curr)

To branch off from curr, we simply try add each subarray from s[i:i+1] to s[i:i+3] to curr and shift to the correct index. The subarray must be validated as a legal segment of an ip before the recursion can continue. Namely, if the value of segment is smaller than 256 and if it is a legal integer (no leading zeros).

We can also early exit the recursion if the remaining number of digits is less than the number of dots still required, but this is kind of overkill IMO.

Implementation

def restore_ip(s):
	if len(s) > 15 or len(s) < 4:
		return []
		
	res = []
	def dfs(i, curr):
		if i == len(s):
			if len(curr) == len(s) + 3:
				res.append(curr)
			return
 
		dot = '' if i == 0 else '.'
		take = ''
		for j in range(i, min(i+3, len(s))):
			take += s[j]
			if int(take) < 256 and not (len(take) > 1 and take[0] == '0'):
				dfs(j+1, curr + dot + take)
			else:
				break
	dfs(0, '')
	return res
	
#time: o(1) because len(s) can never be greater than 15
#memory: o(1)

Mnemonic
Try 3 digits, build the tree.

Visual

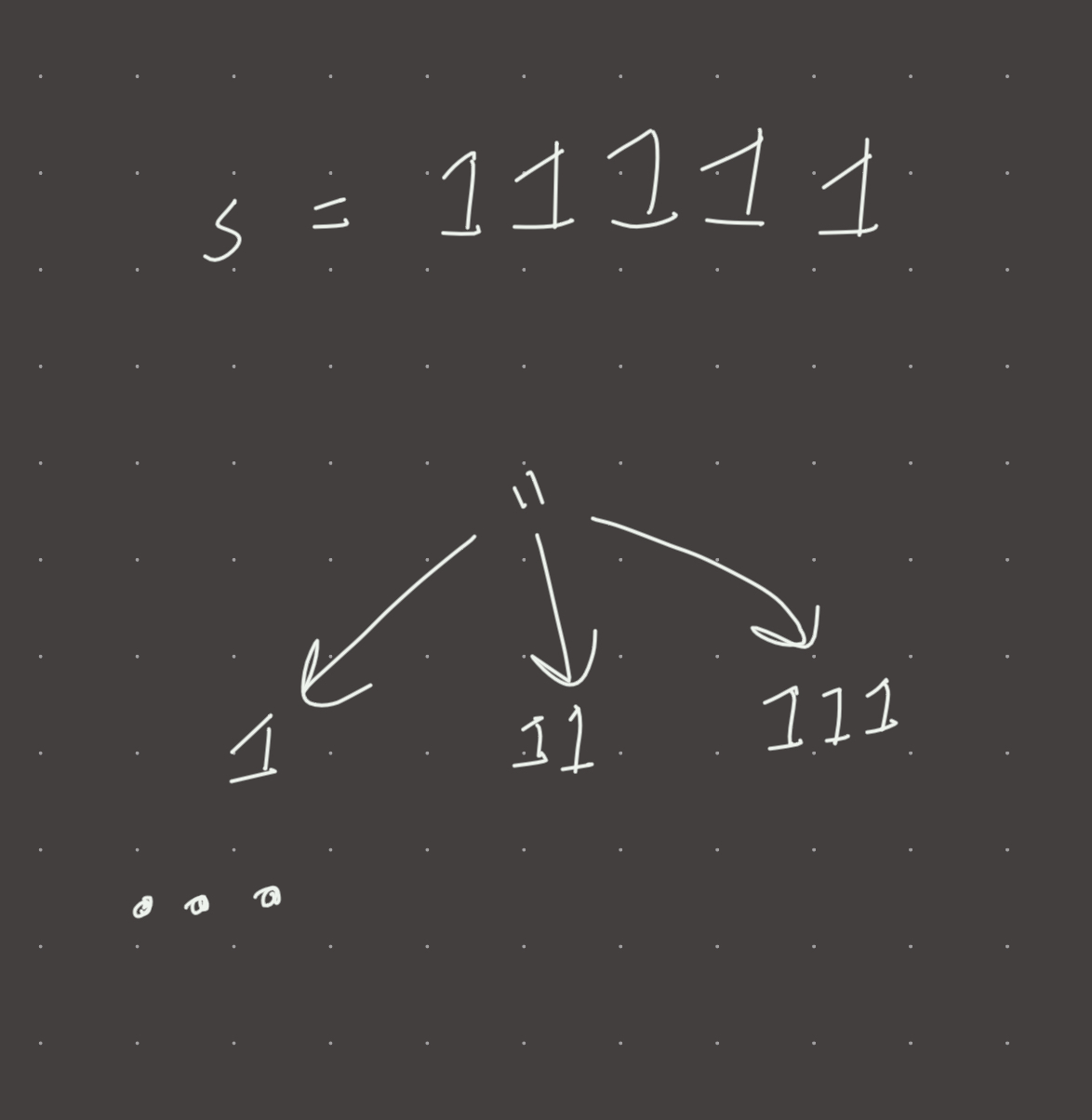
Review 1
This is really a back tracking problem. The above implementation is not great and does not actually use back tracking properly (arguably at all). Here is a much better implementation:

Implementation (back tracking)

def restoreip(s):
	ips = []
	ip = [None, '.', None, '.', None, '.', None]
	def dfs(i, j):
		if i == len(s) and j == 8:
			ips.append(''.join(ip))
			return
		if k == 8:
			return
 
		curr = ''
		for k in range(i, min(i+3, len(s))):
			curr += s[k]
			if len(curr) > 1 and curr[0] == '0':
				break
			if int(curr) > 255:
				break
			ip[j] = curr
			dfs(k+1, j+2)
			ip[j] = None
			
	dfs(0, 0)
	return ips
	

review