Smallest range covering elements from k lists

Link: https://leetcode.com/problems/smallest-range-covering-elements-from-k-lists/

Solution:

DSA: heap

Intuition
The key to understanding this problem is realizing that a valid sequence will have exactly one element from each list. From this valid sequence, the range is (min_val, max_val).

For example:

[1, 4, 7, 10]
[2, 5, 8, 11]
[3, 6, 9, 12]

1,2,3 is a valid sequence with a range 1,3
4,5,6 is a valid sequence with a range 4,6
1,8,12 is also a valid sequence with a range 1,12

So the problem now becomes: how do we choose which elements from each list to put in the sequence? Min heap!

If we keep a min heap of exactly size K and with exactly one element from each list, we would always know what the minimum value is (top of the heap). The maximum value we can just keep in a variable that we evaluate every time we push to the heap. But how do we ensure that the min heap has exactly one element from each list? We pop the top of the heap and add the element next to it back into the heap!

For example:

[1, 4, 7, 10]
[2, 5, 8, 11]
[3, 6, 9, 12]
 
min_heap = [1, 2, 3] # in practice each element will be a tuple (num, row, col)
min_heap = [2, 3, 4] # because we need row, col to get the next element to add
 
#we popped 1 off the heap and added element next to it which is 4!
#now the new range is [2,4]!

Starting from the first column, we can continue in this way until either all elements have been seen, or the top of the heap is the last element in it’s respective list!

Implementation

def smallest_range(nums): #nums is a list of lists
	max_val = float('-inf')
	min_heap = []
	n = 0
	for row in range(len(nums)):
		n += len(nums[row]) - 1
		min_heap.append((nums[row][0], row, 0))
		max_val = max(max_val, nums[row][0])
	heapify(min_heap)
	res = (min_heap[0][0], max_val)
 
	while n:
		_, row, col = heappop(min_heap)
		if col == len(nums[row])-1:
			return res
		max_val = max(max_val, nums[row][col+1])
		heappush(min_heap, (nums[row][col+1], row, col+1))
		if max_val - min_heap[0][0] < res[1] - res[0]:
			res = (min_heap[0][0], max_val)
		n -= 1
	return res

Visual

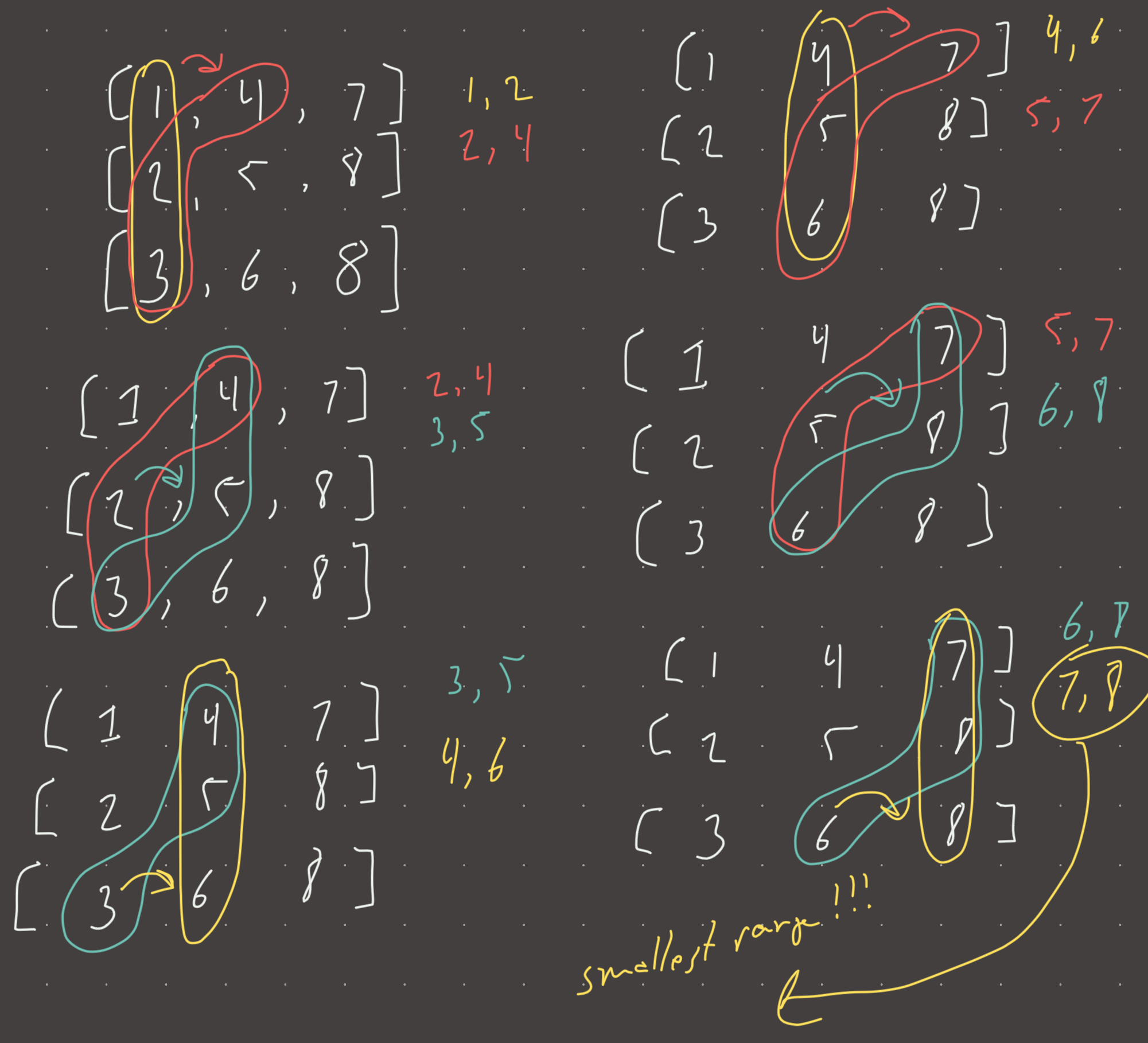
Review 1
Two things to bear in mind:

1. As soon as a row goes out of bounds, we can return the result because the range can only increase!
2. When we pop off the heap, we are shrinking it such that only k elements can be inside, so don’t use the popped element for evaluating the range…instead use the top of the heap after pushing the next element onto the heap!

review