Link: https://leetcode.com/problems/subarray-sum-equals-k/
Solution:
Topics: hash map
Intuition
This is a great little problem! I really enjoyed solving this one because initially I was looking for a constant space solution with a sliding window. Upon further analysis though, it was clear that 2 pointer sliding window could not work. Why?
Consider the array [0,0,1,0,0] and k=1. There are no conditions for growing or shrinking the sliding window because once we get to the window [0,0,1], we can of course shrink the window to count every subarray and correctly count 3 subarrays with sum k in the window. So what’s the problem?
The problem is, after shrinking the window, the sum would be zero and the remaining elements are [0,0]. This is a problem because we can make quite alot more subarrays with sum k by using these remaining zeros: for example [0,1,0] , [1,0,0].
Cases such as this get more plentiful when considering negative numbers. It would seem that we must take the sum of every possible subarray with an n**2 operation…or do we?
Hash map to the rescue! Concealed within this problem is a has/needs pattern that is so common in hash map problems. We can keep a frequency of the current sum as we iterate through nums. We can then compute a complementary sum that, if it has been seen previously, subtracting it from the current sum would equal k! The result is simply incremented by the frequency of the complementary sum!
Implementation
def subarry_sum(nums, k):
res = 0
sums = {0:1}
curr_sum = 0
for num in nums:
curr_sum += num
complement_sum = curr_sum - k
if complement_sum in sums:
res += sums[complement_sum]
sums[curr_sum] = sums.get(curr_sum, 0) + 1
return res
#time: o(n)
#memory: o(n)Mnemonic
Think of subtracting previous partitions from the current one. We don’t know where the partitions end but thats irrelevant to the problem because simply the existence of the partition (with the complementary sum) means that there exists a subarray of some size whose sum amounts to k.
Visual
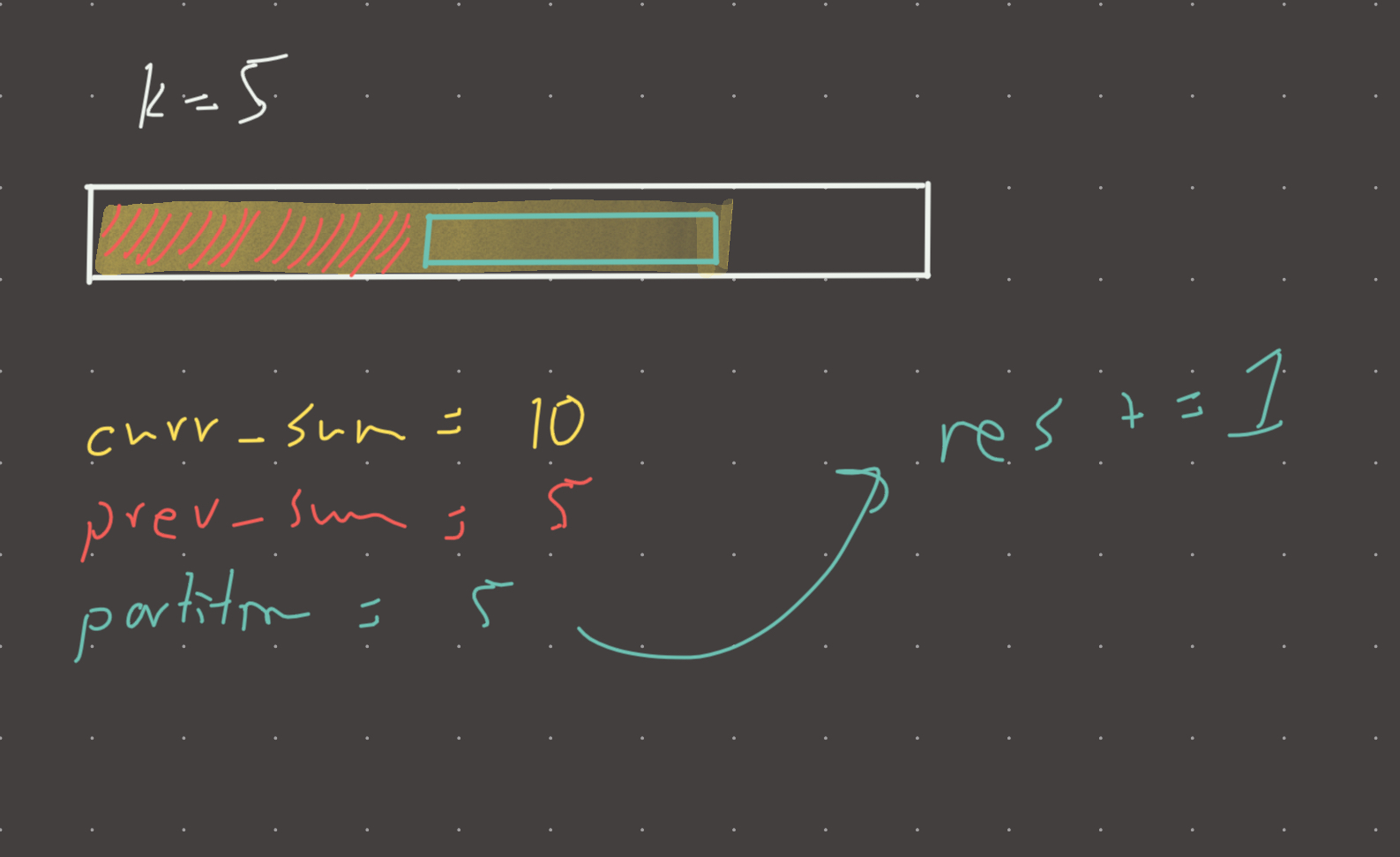
Review 1
Too easy, crushed it. Nice editorial though.
Review 2
Too easy.