Link: https://leetcode.com/problems/the-kth-factor-of-n/
Solution:
Topics: math, factor pair symmetry
Intuition
This is a great little problem for learning some arithmetic theory. Basically, we can iterate over integers 1-n and check if n % i == 0. If the condition is true, this number is a factor. This of course works but it requires us to iterate all the way up to n. This can be problematic if n is extremely large; the constraint for n is only 1000 in this problem… but we can implement a more optimal solution.
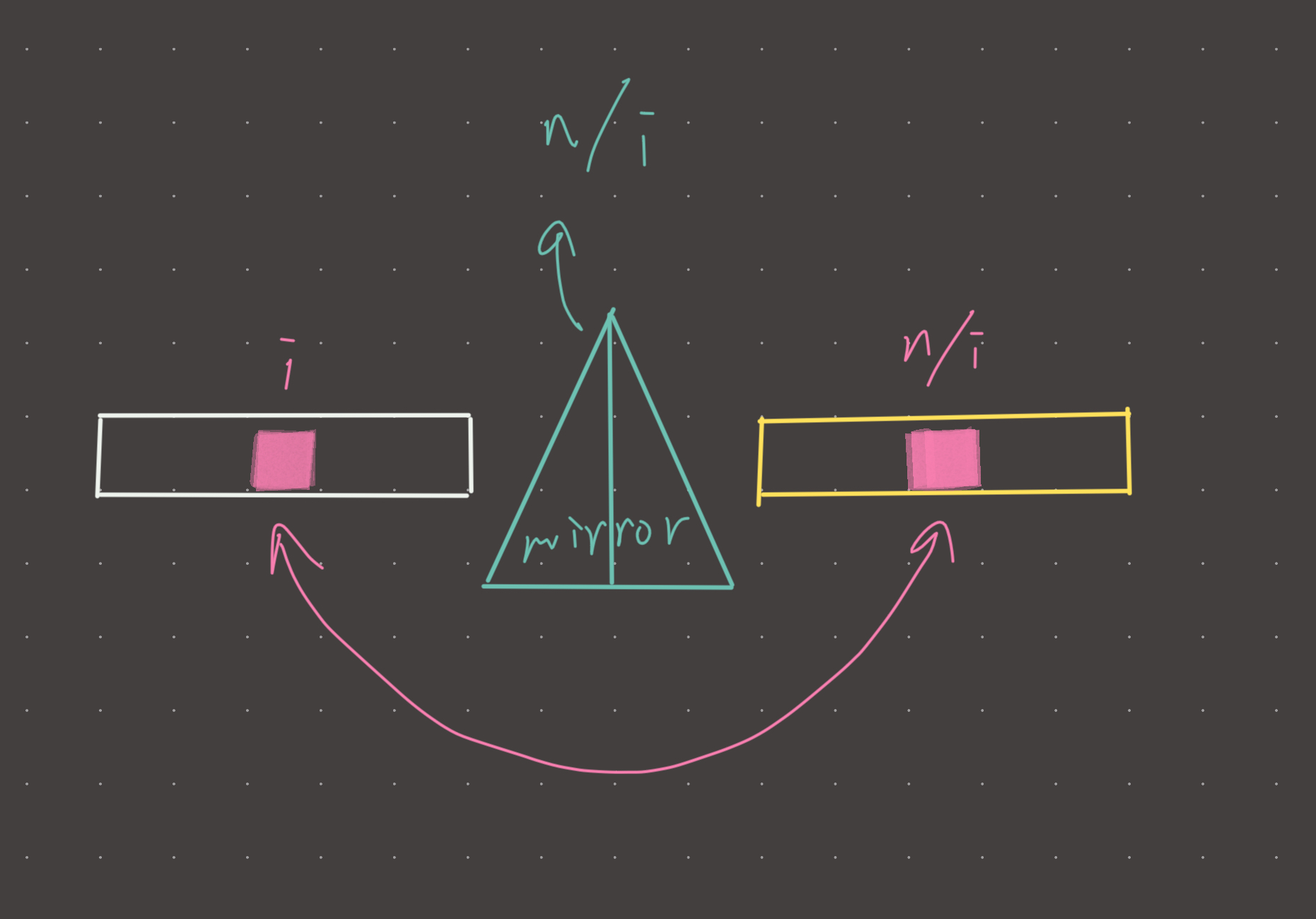
We can use a the symmetric property of factors to generate all factors in o(sqrt(n)) time! What is factor pair symmetry?
n = 12
A = 2
If A is a factor of 12, then 12/A is also a factor of 12. 12/2 = 6.
This is because n = A * B
Therefore B = n/A
How does this help us? Well, we can use factor pair symmetry to iterate from 1-sqrt(n) to get the smaller factor, and when the smaller factor is found, we use it to generate it’s symmetrical larger pair!
For example:
n = 12
int_root = 3
i | smaller | larger
------------------------
1 1 12
2 2 6
3 3 4
We can see that all factors of 12 can be generated in this way. If we append the smaller and larger to serarate lists, we can combine them (with the larger reversed), to form a sorted list of all factors!
The Kth element in that factor array is the result!
Lets look an an edge case:
n = 9
int_root = 3
i | smaller | larger
------------------------
1 1 9
2 - - <--- 2 is not a factor
3 3 3 <--- larger == smaller (duplicate)
When i = 3, we risk adding a duplicate factor because i == n/i. Basically we need to check for this condition before adding. It will only happen on the last iteration and only for numbers that are perfect squares (4, 9, 16..).
Implementation
def kth_factor(n, k):
small = []
big = []
for i in range(1, int(sqrt(n))+1):
if n % i == 0:
small.append(i)
if i != n // i:
big.append(n // i)
factors = small + big[::-1]
if k > len(factors):
return -1
return factors[k-1]
#time: o(sqrt(n))
#memory: o(2sqrt(n))Visual
Review 1
Cool problem! Remembered the optimal solution here. What is factor?
A = B * C
B and C are factors of A.
So if we know A and we know B, then we can derive C.
C = A / B
What we are doing here is finding the smaller factor, and then generating the larger factor.