Link: https://leetcode.com/problems/trapping-rain-water/
Solution:
Topics: greedy, two pointer
Intuition
This is a very nice two pointer problem! It can be done in two passes (forwards and reverse), but the two pointer solution in way more elegant. The key idea is to traverse from both sides and keep the max_height on the left and max_height on the right. We move the pointer left if the l_max is smaller than the r_max…this is because we want to end the algorithm at the peak (or a peak) to ensure all sections of water are counted. This is the case because the algorithm will rely on a r_res and l_res to keep track of the quantity of water in the respective portion. When a new l_max or r_max has been reached, l_res or r_res respectively will be added to the overall result. Therefore, for all sections of water to be counted, the algorithm must ensure that l and r pointers end on the (or a) peak.
For example:
Lets do this with only one pointer to demonstrate the issue.
|
| | |
^
res = 0
temp_res = 0
max_height = 1
|
| | |
^
res = 0
temp_res = 1 (temp_res += max_height - current_height)
max_height = 1
|
| | |
^
res = 0
temp_res = 2
max_height = 1
|
| | |
^
res = 2 (res += temp_res)
temp_res = 0 (temp_res = 0)
max_height = 2
|
| | |
^
res = 2 (res += temp_res)
temp_res = 2 (temp_res = 0)
max_height = 2
|
| | |
^
res = 2 (res += temp_res)
temp_res = 4 (temp_res = 0)
max_height = 2
|
| | |
^
res = 2 (res += temp_res)
temp_res = 5 (temp_res = 0)
max_height = 2
The algorithm ends with result of 2. So it worked as expected before the pointer reached the peak, but as soon as the peak became the max_height, no more water was counted because the algorithm will only add temp_res to res when a new max_height is seen.
Furthermore, our algorithm ends with temp_res = 5, which would only make sence if a new max_height will be seen later on.
So the idea here is to implement this algorithm with a pointer moving left, and a pointer moving right while ensuring that the pointer with the smaller max_height is the one that is moved. This way the algorithm always ends and the peak for both pointers and thus will work as expected.
Its important to note that instead of 2 pointer we could just do two passes and end at the (or a) peak max(height)…the effect would be the same.
Implementation
def trap_water(height):
res = 0
l = 0
r = len(height)-1
l_max = height[l]
r_max = height[r]
l_res = 0
r_res = 0
while l < r:
if l_max < r_max:
l += 1
if height[l] >= l_max: #or equal because you can have this:
l_max = height[l] # |___|__|___|
res += l_res
l_res = 0
else:
l_res += l_max - height[l]
else:
r -= 1
if height[r] >= r_max:
r_max = height[r]
res += r_res
r_res = 0
else:
r_res += r_max - height[r]
return res
#time: o(n)
#memory: o(1)Mnemonic
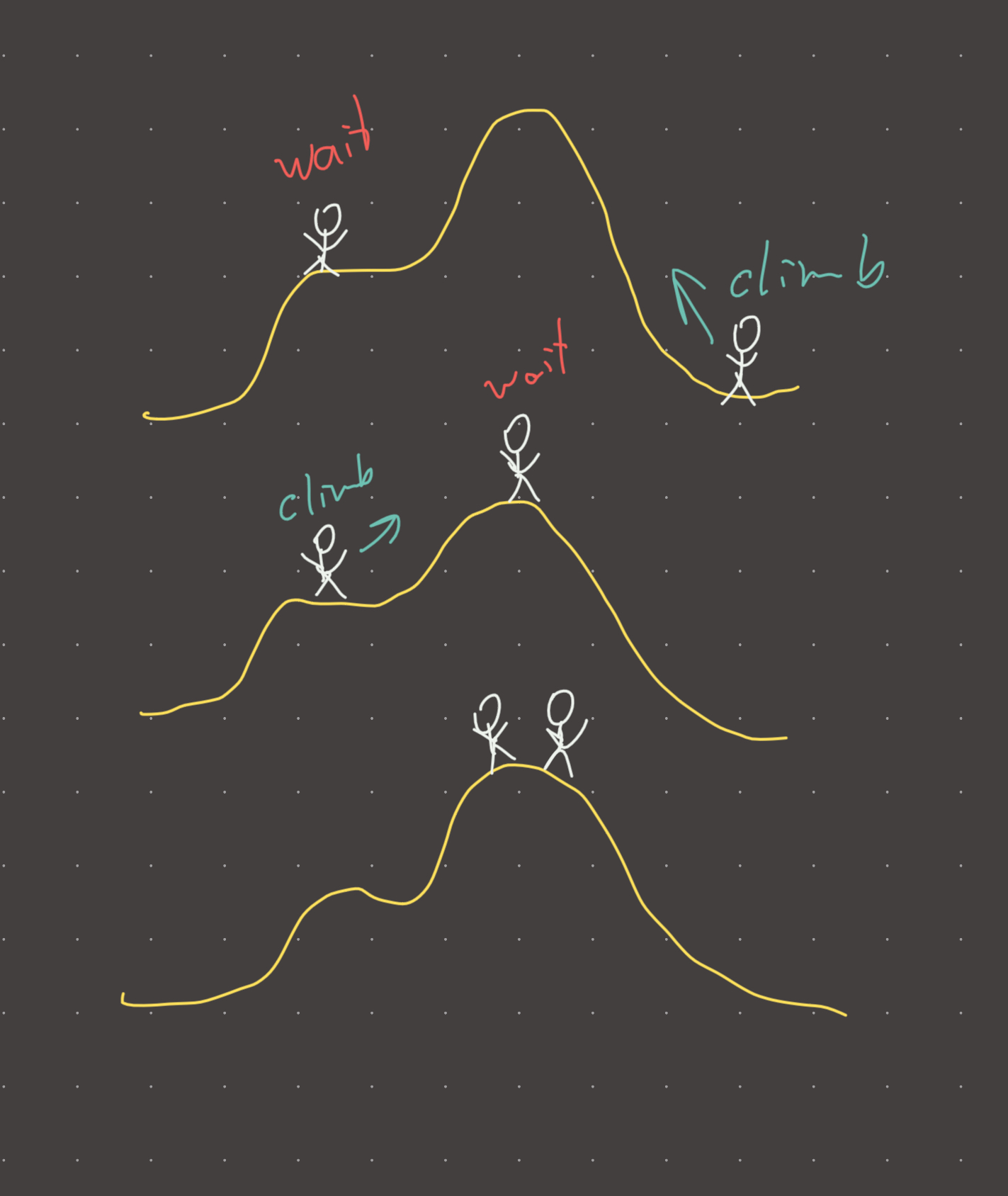
You and a friend are climbing a mountain from opposite sides. You have an agreement that whoever reaches the peak first has to wait for the other person. Unfortunately you are both blind and wont necessarily know if the peak has been reached, so its not clear when to stop. Fortunately you have access to each other’s altitude. So, while your altitude is lower than your friend, you climb…if not, you take a break. This will guarantee that you both end up at the peak of the mountain.
Visual
Review 1
I don’t know how many times I have solved this problem, but every time I get destroyed by the edge cases. I have realized why this is the case after seeing the implementation above. Simply put, this is the ugliest and weirdest code that I have ever seen in my life. Why? Well lets start with while l < r:…this is weird and rarely used, prefer while l <= r:. Also, incrementing the pointers at the start of the conditional should be punishable by jail. These are contrived devices I came up with to deal with edge cases. No chance to come up with these in an interview.
The two-pointer implementation in the editorial is too clever and I think not generic enough for followups. Also the stacks implementation feels extremely contrived.
I’m going to solve this once and for all with a non-contrived implementation that is not too clever and is also generic. The key is to compute l_max and r_max FIRST and THEN shift the pointers depending on which is greater. This has the benefit of greatly simplifying the code while also staying generic for followups like “which cavity holds the most water”.
def trap_rain(height):
res = 0
l = 0
r = len(height)-1
l_max = 0
r_max = 0
l_res = 0
r_res = 0
while l <= r:
if height[l] >= l_max:
res += l_res
l_res = 0
l_max = height[l]
if height[r] >= r_max:
res += r_res
r_res = 0
r_max = height[r]
if l_max < r_max: #this gets evaluated even when a new max was just
l_res += l_max - height[l] #found, it evaluates to 0.
l += 1
else:
r_res += r_max - height[r]
r -= 1
return res