Link: https://leetcode.com/problems/ugly-number-ii
Solution:
Intuition
To solve this problem, we must make a key observation about ugly numbers. An ugly number can always be formed by multiplying a previously seen ugly number by either 2, 3 or 5…and by definition, the first ugly number is 1. This is actually all we need to solve the problem. There is also a DP solution but I wont go into it.
For example:
uglies = [1]
the only ugly number seen so far is 1, so knowing that all ugly numbers can be formed by muliplying a previously seen ugly number by either 2, 3 or 5, we can generate the potential next ugly number:
potential_next = 1*2, 1*3, 1*5 ---> 2, 3, 5
So the question now is which one to choose from? The next ugly number is always the SMALLEST of the potentially next numbers, but we dont discard the other ones because they could be the next after this one!
So choosing the smallest and removing it from potientials:
uglies = [1, 2]
potential_next = [3, 5]
Contained within our pool of potentials, is every possibility that is formed with 1, but now we have seen a 2, so we must generate the next set of potentials that can be formed by multiplying 2 with 2,3,5!
potential_next = [3, 5, 4, 6, 10]
Take the smallest again...
uglies = [1, 2, 3]
petential_next = [5, 4, 6, 10]
do this n times, result will be uglies[-1]...
So the idea here is to continuously maintain a pool of potential next ugly numbers, and always take the min. The natural choice is a min heap to maintain the pool.
If its still not clear then take a look at a variation on this problem…lets say we already have a list of n uglies and the task is to find the next. How would it be done?
uglies = [1,2,3,4,5,?]
We know that the next ugly number can be made by mulitiplying a previously seen ugly number by 2, 3 or 5... so lets do it
1 --> 2,3,5
2 --> 4,6,10
3 --> 6,9,15
4 --> 8,12,20
5 --> 10,15,25
One of these numbers is the next ugly number...but which one?
We know that the next ugly number must be greater than the current one...which in this case is 5...so lets filter the potential numbers:
2 --> 6,10
3 --> 6,9,15
4 --> 8,12,20
5 --> 10,15,25
Out of these potential numbers we take THE SMALLEST, so the next ugly number is 6!
If its still not clear, by using heap we are doing exactly the same processing as above, but it’s done continuously since we are building the uglies iteratively and one at a time! So for each new ugly number seen, we are updating the pool with uglies that may be seen in the future!
Implementation
def ugly_num2(n):
seen = {1} #keep a set to prevent duplicates in the heap
min_heap = [1] #top of the heap is always the current
for _ in range(n-1):
current = heappop(min_heap)
for prime in [2, 3, 5]:
if prime*current not in seen:
heappush(min_heap, prime*current)
seen.add(prime*current)
return heappop(min_heap)
#time: o(nlogm) m is the size of the heap
#memory: o(m)Mnemonic
You go to a beauty salon and there are 3 makeup artists, so you clone yourself 3 times and work with each. The clone that looks most similar to the original state becomes the “leader”. The new leader is cloned again and each clone works with the 3 designers. The clone that looks closest to the original is chosen (we choose among the new clones and the old ones).
Visual
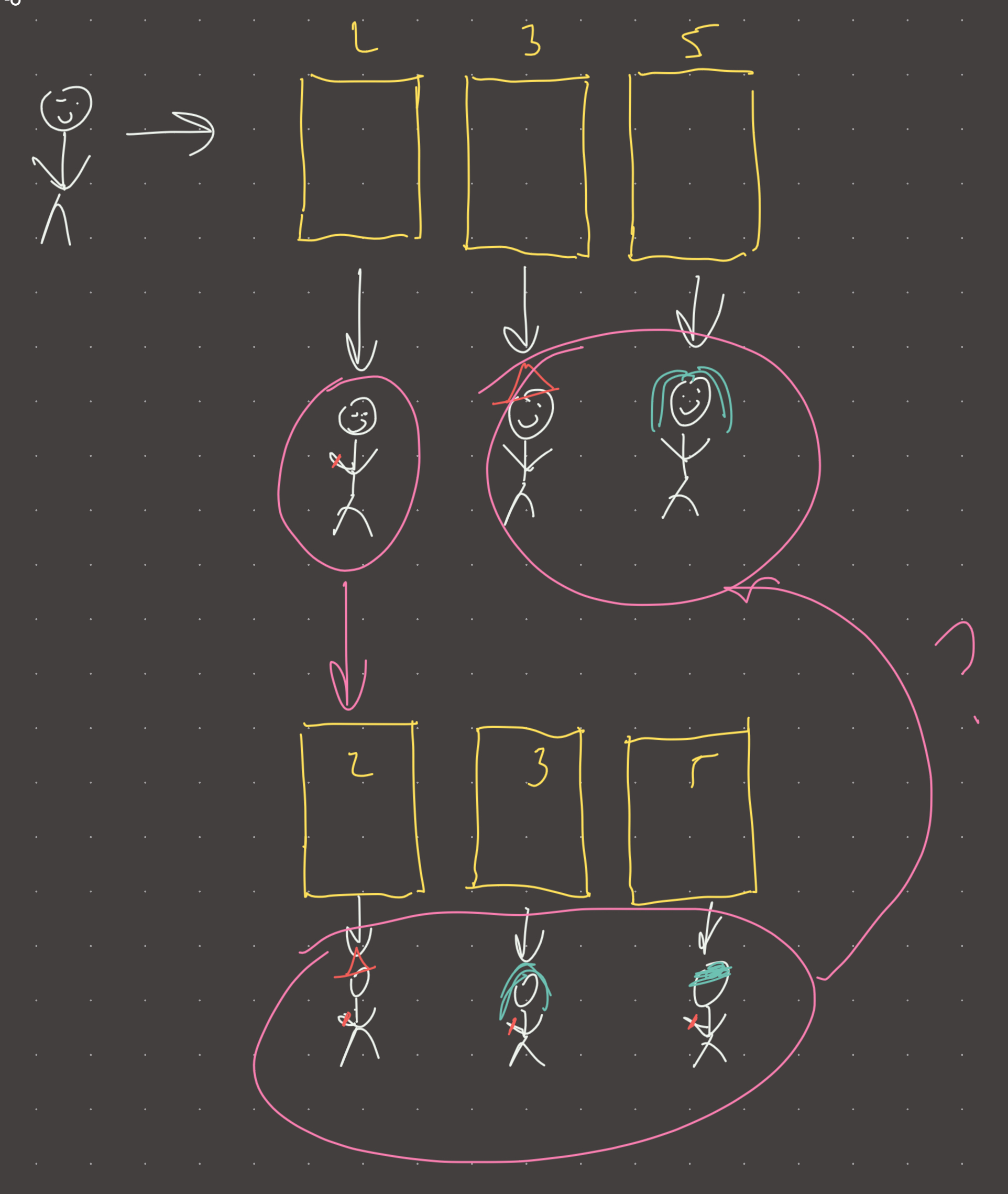
Review 1
I confused this with another problem from memory, so I wasted alot of time. After I stopped trying to solve the problem through (faulty) memory, I found the heap solution very fast. Remember that we can encounter duplicates, so keep a visited set. I’m tagging this hard because of how much time I wasted here.
Review 2
Crushed it very fast.