Link: https://leetcode.com/problems/uncrossed-lines/
Solution:
Intuition
This is a relatively tricky problem, but kind of straight forward once you realize that the correct approach is dynamic programming. How do we realize this?
The first clue that leads to DP is understanding that if we make a connection, that connection could disallow more future connections. What is the optimal configuration strategy?
For example:
nums1 = [1,2,2,2]
nums2 = [2,2,2,1]
If we connect the ones, it would dissallow all future connections between 2's
[1,2,2,2]
\
\
\ This connection spans the entire arrays
\
\
[2,2,2,1]
The optimal choice is to skip the 1's and connect the 2's
[1,2,2,2]
/ / / We can make 3 connections
[2,2,2,1]
We already get the sense that there is no local greedy decision that can be made because our greedy algorithm we would need perfect knowledge of all future elements in both arrays…which would make it not greedy at all.
The above example points to a take/skip strategy which is so common in DP patterns. We can either make a connection or not make a connection.
The other hint at DP is the fact that we can imagine many configurations of connected arrays as leaves in a binary tree. Our task then is just to pick the one with the most connections (in the most efficient way). I chose to visualize this hint in the visual section.
The implementation kind of writes itself at this point when you map the problem onto the take/skip DP pattern.
Implementation
def uncrossed_lines(nums1, nums2):
@cache
def dfs(i, j):
if i == len(nums1) or j== len(nums2):
return 0
take = 0
for k in range(j, len(nums2)):
if nums1[i] == nums2[k]:
take = 1 + dfs(i+1, k+1)
break
#no need to look further, as the first connection seen
#disallows the least number of connections, so if this
#connection is not worth making then by definition all
#other connections in front of it would also not be
#worth making
leave = dfs(i+1, j)
return max(take, leave)
return dfs(0, 0)
#time: o(n*m)
#memory: o(n*m)Visual
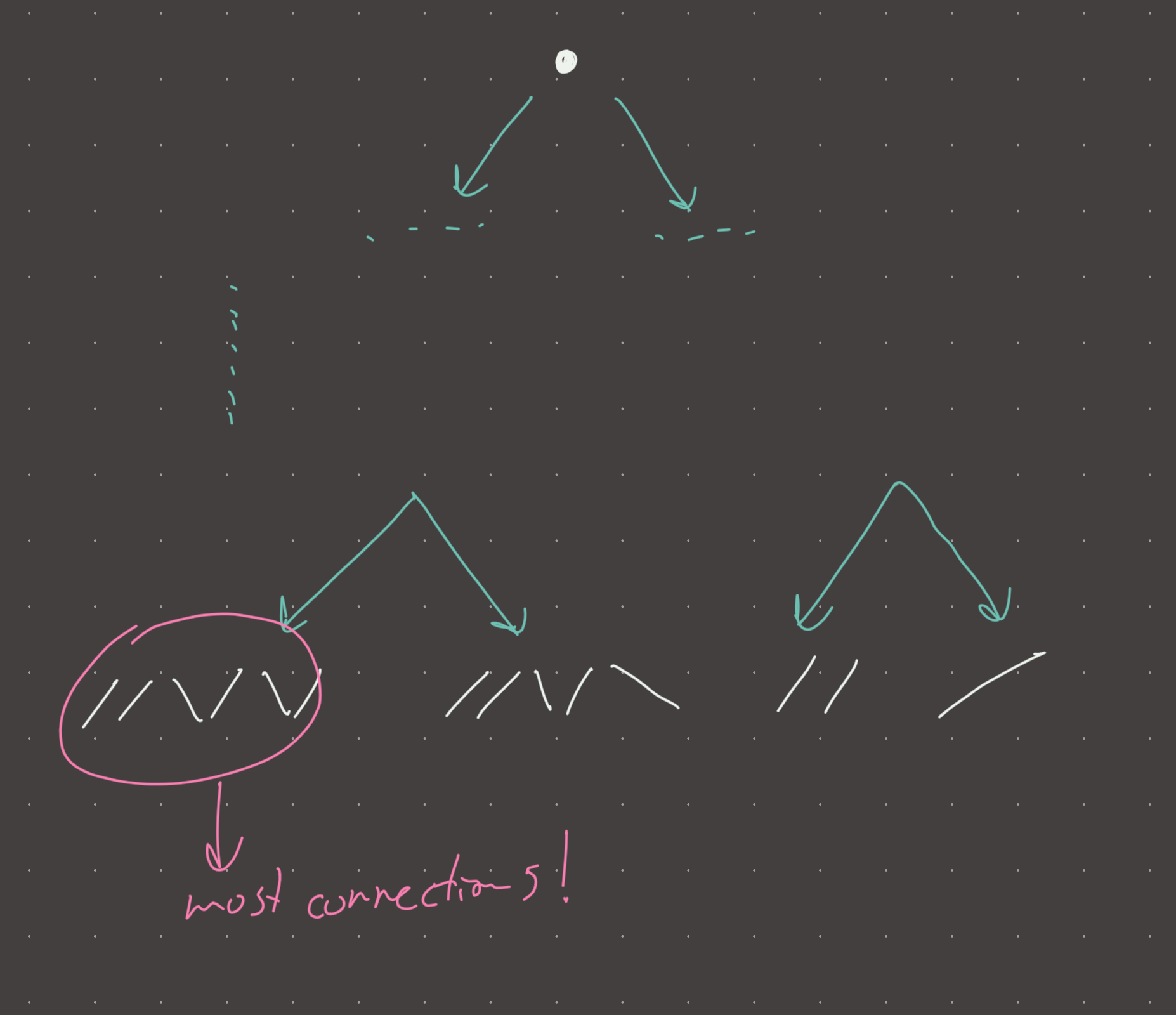
Review 1
I pretty much figured out the correct approach from the start but there were two things I missed before running the test cases:
- When you make a connection, you also have to not make the connection.
- You only need to consider the first match seen, as the first match leaves the most possibilities open for future matches (and thus connections).
Im tagging this one hard simply because IMO the recursion setup is kind of subtle.
Review 2
Crushed it easily.