Validate binary tree nodes

Link: https://leetcode.com/problems/validate-binary-tree-nodes/

Solution:

Topics: BFS, set

Intuition
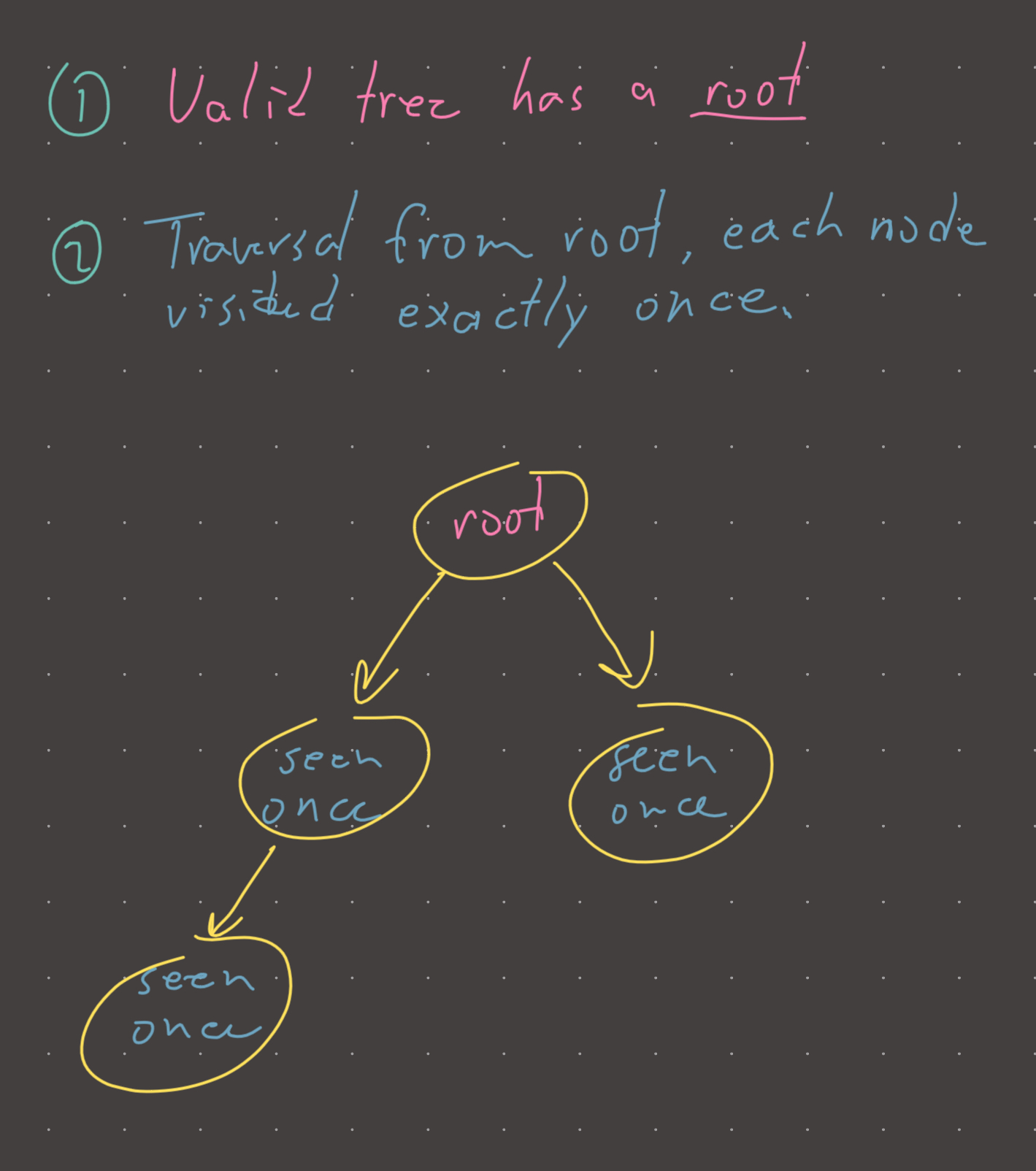
I struggled with this problem a little bit, but when I started thinking about it in terms of what constitutes a valid binary tree, the approach became clear. A binary tree MUST have a root and if we traverse from the root, there must be no cycles.

So with these two axioms, the solution almost writes itself. First we find the root (only node with no parent), then we traverse the tree starting at the root and if we detect a cycle, return the tree is invalid. We can traverse either with DFS or BFS… it functionally makes no difference so choose BFS for efficiency.

The notable edge case is where there are no cycles but there are unvisited nodes…which would indicate multiple trees/components (also invalid).

Implementation

def validate_nodes(n, leftChild, rightChild):
	root = {node for node in range(n)}
	root = root ^ set(leftChild)
	root = root ^ set(rightChild)
	if len(root) != 1:
		return False
		
	seen = set()
	queue = deque([root.pop()])
	while queue:
		node = queue.popleft()
		if node == -1:
			continue
		if node in seen:
			return False
		seen.add(node)
		queue.append(leftChild[node])
		queue.append(rightChild[node])
	return len(seen) == n
		
#time: o(n)
#memory: o(n)

Visual

Review 1
Challenging problem. I got trapped in the out/in degree strategy used in Town judge before realizing that out/in degree does not work on validating binary trees. Why? Because in/out degree doesn’t care about cycles! While it’s possible to identify the root and correct number of connections using in/out degree, nothing can be done about cycles because in/out degree is a counting strategy and not a traversal.

But out degree is not completely useless. We can use it to identify the root and then traverse the tree starting at the root while keeping a visited set. There is a cycle or multiple parents if a node has been seen! Why? Because in a DFS traversal on a valid tree, every node is seen exactly once. So while in graph cycle detection we require visiting/visited sets, for trees this is overkill because the nature of the tree is that each node can only have one parent. In a graph, nodes can have multiple parents so cycle detection is more involved.

Also, check the length of the visited set. It should be equal to n, otherwise there are disconnected components (and potentially valid ones, but we are looking for a single tree).

review
hard