Arithmetic slices

Link: https://leetcode.com/problems/arithmetic-slices/

Solution:

Topics: greedy, subarray, reservoir

Intuition
Basically this is what I like to call a reservoir pattern. If an arithmetic slice contains N slices, then a newly added element creates exactly N+1 more slices. In other words, our current reservoir gets reabsorbed every time our slice grows (and plus one).

For example:

[1,2,3] #there is exactly 1 arithmetic slice
[1,2,3,4] #now there are 3 arithmetic slices (current + (current + 1)). Why?
 
[1,2,3] #slice 1
[2,3,4] #slice 2
[1,2,3,4] #slice 3

When our slice ends, we just set our current variable to 0, signifying that we are no longer counting an arithmetic sequence.

Implementation

def num_arithmetic_slices(nums):
	res = 0
	current = 0
	for i in range(2: len(nums)):
		if nums[i] - nums[i-1] == nums[i-1] - nums[i-2]:
			current += 1
			res += current
		else:
			current = 0
	return res
			
#time: o(n)
#memory: o(1)

Visual

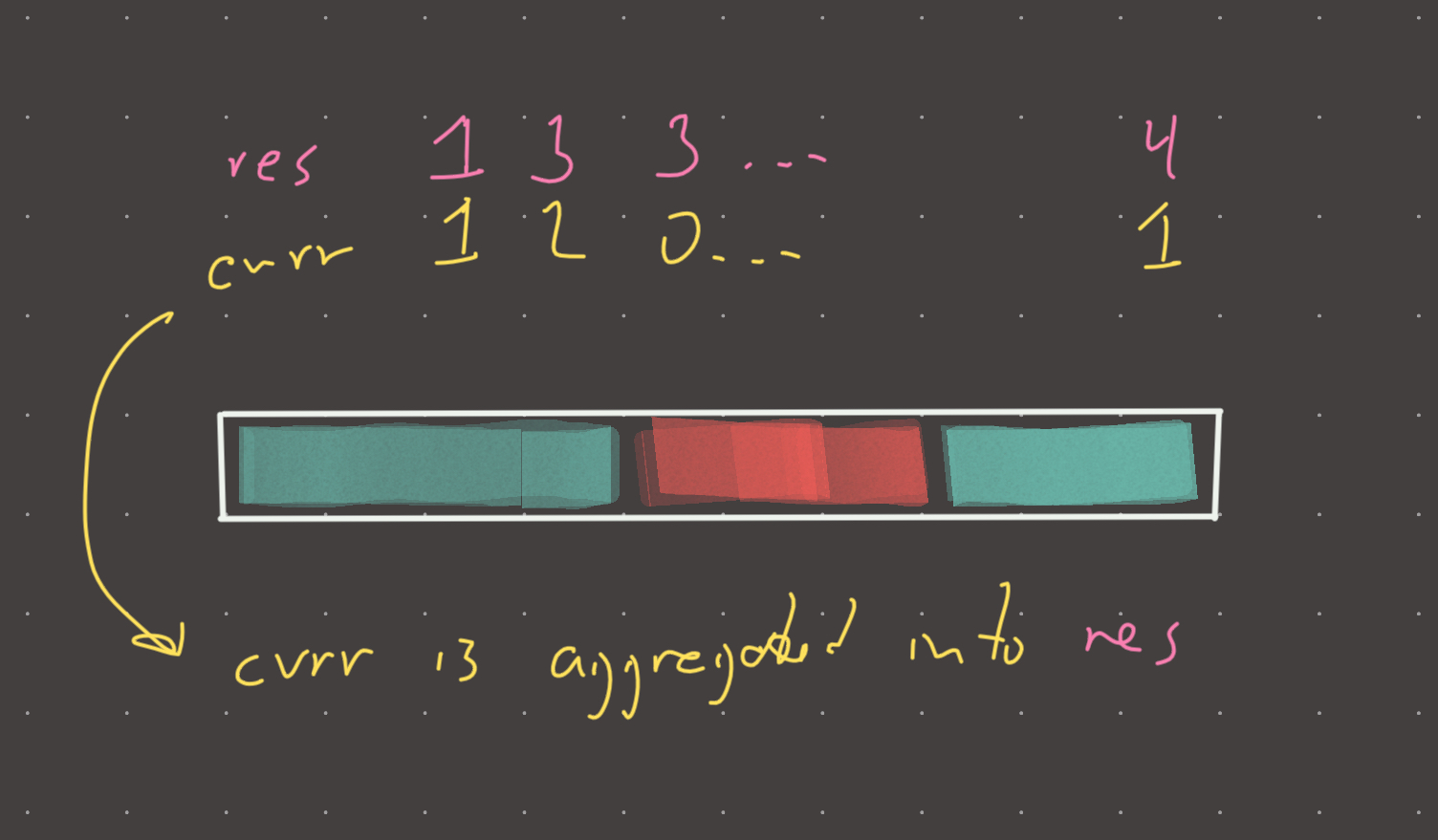
Review 1
Again, not reading the problem and assuming that I know what an arithmetic sequence is has bitten me in the ass. For whatever reason I thought I remembered this problem and falsely assumed that an arithmetic sequence is if 3 elements are increasing or decreasing by 1 (1,2,3,4)…this is obviously not the case. An arithmetic sequence is any sequence that is increasing or decreasing consecutively by the same number for example:

1,2,3,4

2,4,6,8

100, 200, 300

-1, -2, -3

Other than the stupid oversight, I got the “reservoir” pattern correct.

review