Arithmetic slices II

Link: https://leetcode.com/problems/arithmetic-slices-ii-subsequence/

Solution:

Topics: subarray, hash map, Arithmetic slices

Intuition
This is a very tricky problem. The idea is to keep a hash map for each index and keep a count of each difference between the current element and previous elements seen before it. Basically if in the future that difference is seen again, we have formed a valid arithmetic subsequence.

In principle, the implementation is fairly simple but the intuition to come up with this solution, I would say is very hard.

Implementation

def arithmetic_subs(nums):
	res = 0
	diffs = [{} for _ in range(len(nums))]
	for i in range(1, len(nums)):
		for j in range(i):
			diff = nums[i] - nums[j]
			diffs[i][diff] = diffs[i].get(diff, 0) + 1
			if diff in diffs[j]:
				res += diffs[j][diff]
				diffs[i][diff] += diffs[j][diff]
	return res
 
#time: o(n**2)
#memory: o(n**2)

Visual

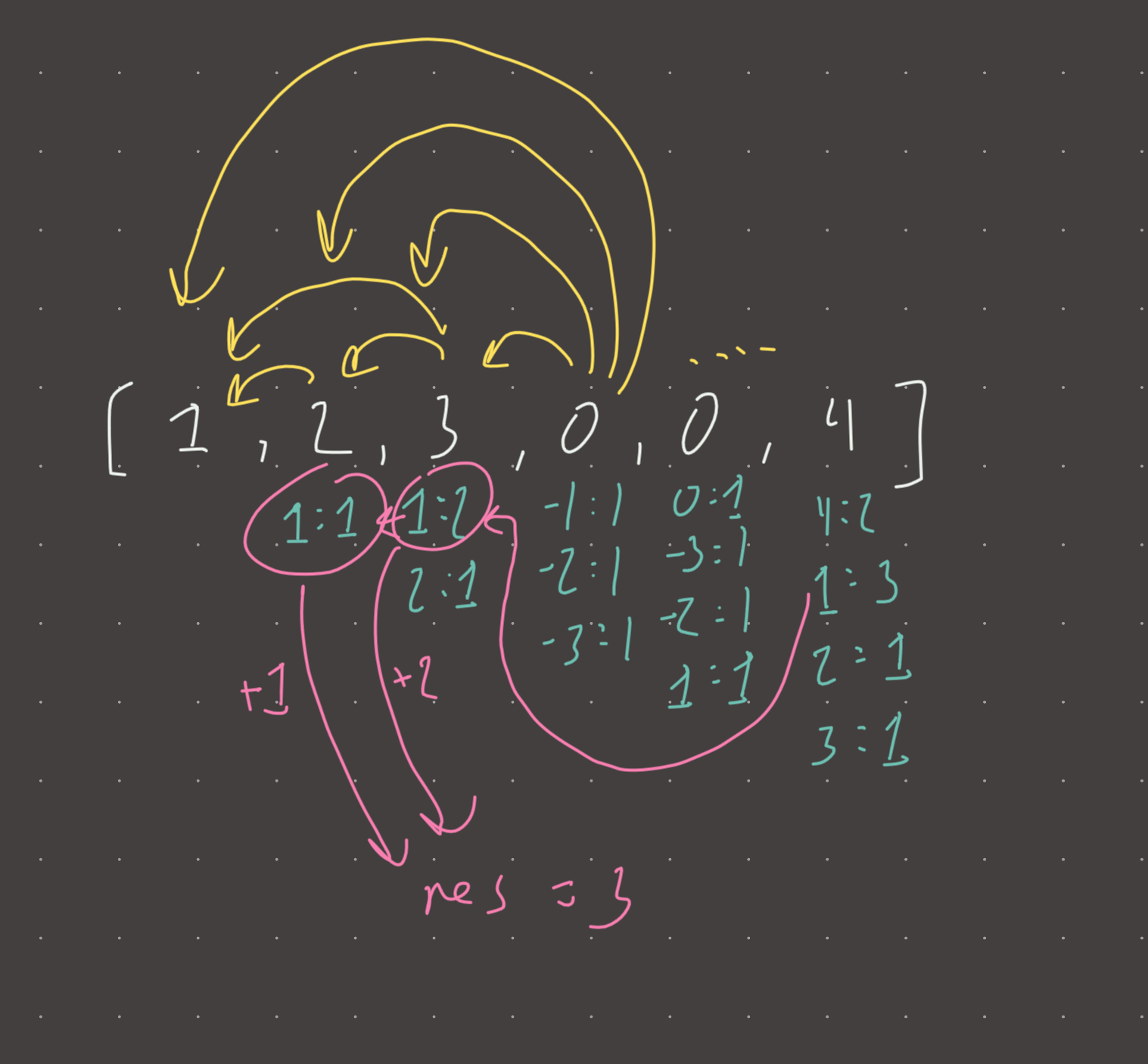
Review 1
Insane problem. I figured out the right approach but could not remember/figure out how to implement it correctly such that the right amount of subsequences are calculated.

Basically, we keep a hash map of counts for every index. This hash map stores the counts of differences seen so far (iterating up to i). If a difference has already been seen at the j index, we add the count to the result, and then add that count to the current hash map value at the difference key! Why do we do this?

Well, adding the count to the result makes sense because if the count is 1, it means the difference has already been seen so therefore the length of the subsequence is 2…so with the current, that makes for a valid arithmetic sequence of length 3!

So then why do we add the seen value to the current hash map? Because this is akin to storing the number of arithmetic sequences that can be made with that difference and that index. This is the “reservoir”.

Overall this problem is very confusing, but still a great one.

review
hard
insane