Champagne tower

Link: https://leetcode.com/problems/champagne-tower/

Solution:

Topics: simulation

Intuition
The idea here is to create a model of this tower and pour the excess at each cup down a level (except at the final level), and then return the value at tower[query_row][query_col]. There are two edge cases to watch out for.

1. The value in a cup can never go negative.
2. The value in a cup can never be greater than one.

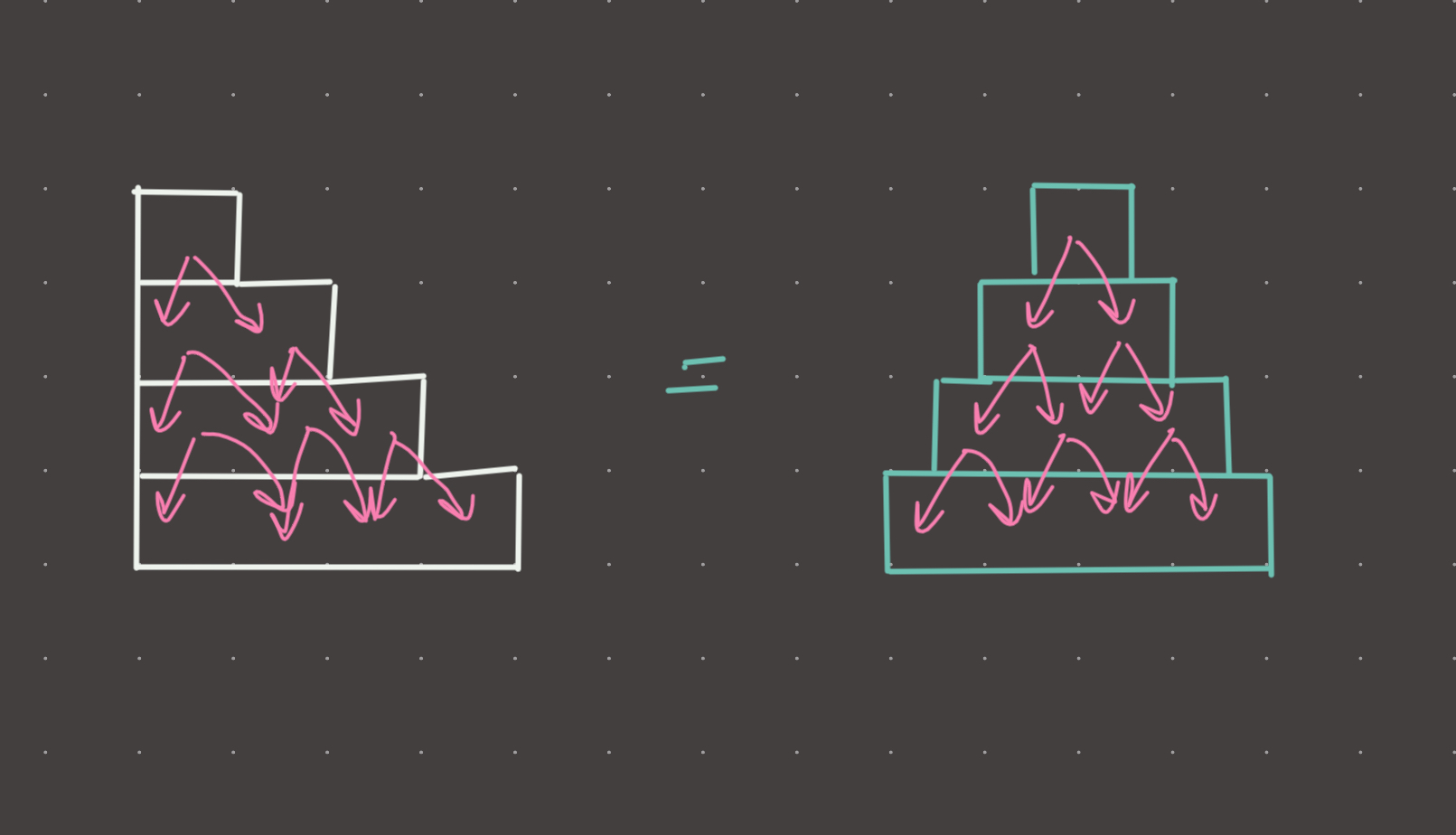
Note that this is NOT a tree, its the diagonal of a matrix…levels don’t double, they increment by one. Similar to the matrix traversal we do for transposing (see Rotate image)

Implementation

def champ_tower(poured, query_row, query_glass):
	tower = [[0]*(i+1) for i in range(query_row+1)]
	tower[0][0] = poured
 
	for level in range(len(tower)-1):
		for pos in range(len(tower[level])):
			overflow = (tower[level][pos] - 1) / 2 
			if overflow > 0:
				tower[level+1][pos] += overflow
				tower[level+1][pos+1] += overflow
	return min(tower[query_row][query_glass], 1)
 
#time: o(n**2) n is the number of levels to the champagne tower 
#memory: o(n**2)

Visual

Review 1
Remember that a cup can have up to two parents that feed it champagne, so we must set up the tower to reflect the reality. Each row is one longer than the previous. A cup’s left child is simply tower[row+1][col], and right child is tower[row+1][col+1].

This is not too different from the configuration in Kth symbol in grammar except in that problem the tree is 1-indexed and a child can only have one parent.

review