Link: https://leetcode.com/problems/k-th-symbol-in-grammar/
Solution:
Topics: tree
Intuition
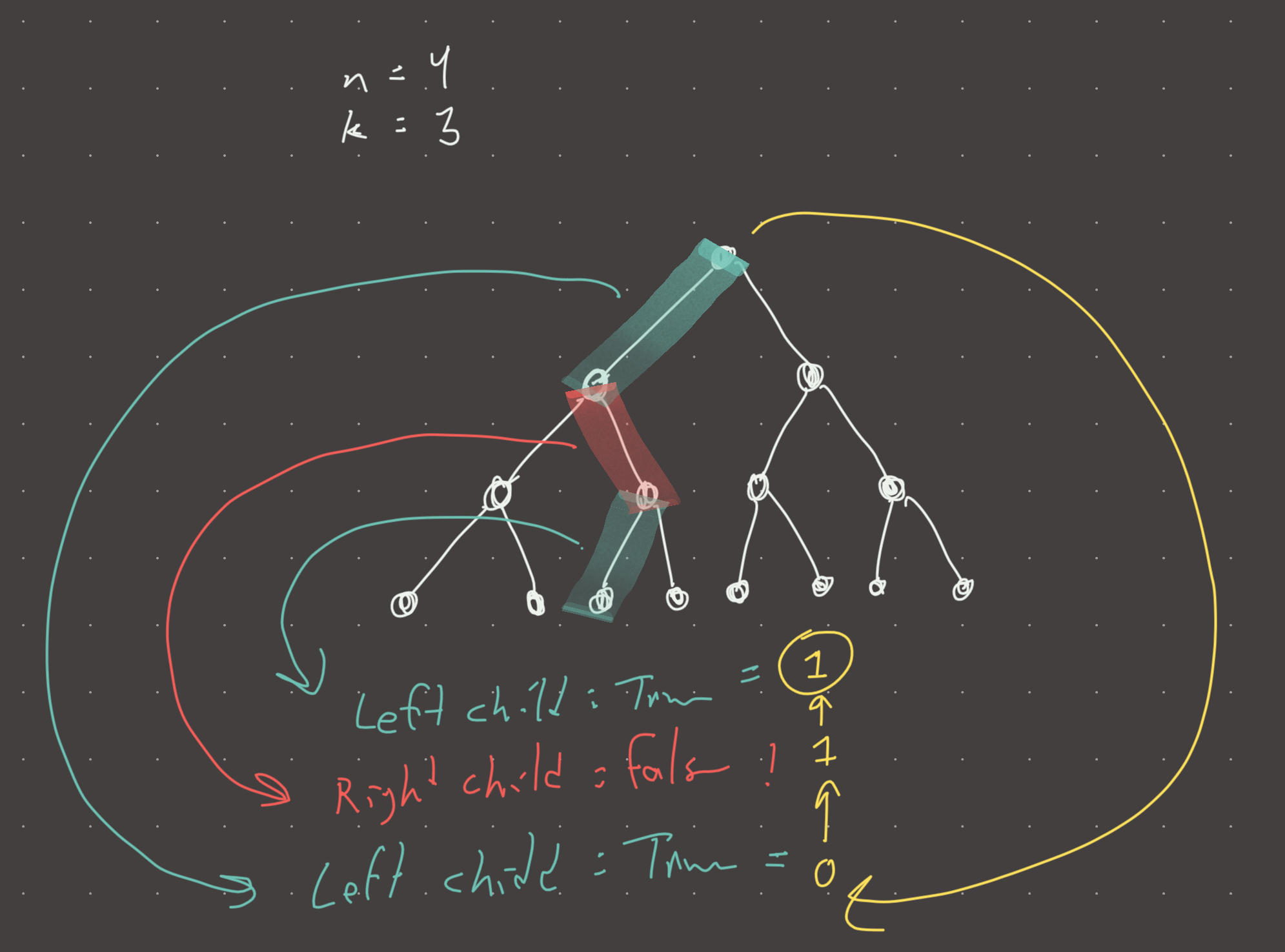
This is quite a tricky problem, but there is actually a very intuitive solution. The key intuition is that when we build out this tree, the left child keeps the same value as the parent and the right child flips the parent value.
0
0 1 #left child is 0 (same), right child is 1 (flipped)
With this insight, we can trace the path back up the tree from the kth symbol at level n back up to the root and evaluate it.
For this solution we convert k to the absolute index in the tree, by adding to it the number of nodes in the levels above with the formula num_nodes = 2**(n-1)-1. We do this to then find the absolute position of each parent with the formula k//2. In the solution we will do this iteratively until k = 1…which would indicate that we have traversed all the way back up to the root.
0
0 1
0 1 1 0
^
# ^ is the target, and it is the 2nd symbol in row 3. (1-indexed)
# the absolute positon is 5 which is obtained by adding the number of nodes in the previous levels to k. index = k + 2**(n-1)-1
# the absolute position of the target's parent is 5 // 2...which is 2, and indeed the 0 above the target is at index 2 of the tree (1-indexed).
If k % 2 == 0, then the node is a left child, otherwise its the right child. We must update our evaluation logic accordingly to keep track of the flips. We do this until k == 1.
Implementation
def kth_symbol(n, k):
if k == 1: #handle edgecase
return 0
index = k + 2**(n-1)-1 #get absolute position
curr = True
while index > 1:
curr = curr if index % 2 == 0 else not curr #flip if right child
index = index // 2 #get parent's position
return 0 if curr else 1
#time: o(n) n = number of levels
#memory: o(1)Visual
Review 1
The solution above is overly complicated. There is no reason to convert to “absolute” index, however the overall approach is correct. What I missed the last time around is that we can easily recover the parent’s position in the row with a slight modification of the parent-child-index relationship:
Normal tree with no rows, only indices:
1
2 3
4 5 6 7
leftchild = parent*2
rightchild = parent*2 + 1
1-indexed row/col tree:
1
1 2
1 2 3 4
leftchild = parent/2 - 1
rightchild = parent/2
Since we are traversing from child to parent, we must get the parent k value to go up the tree. Using the above, we can derive this formula for computing the parent:
parent_k = ceil(k/2)
or...
parent_k = (k+1)//2
Implementation (the easy way)
def kthgrammar(n, k):
def dfs(n, k):
if n == 1:
return True
parent_k = (k+1)//2
if k % 2 == 0: #left child
return not dfs(n-1, parent_k)
else:
return dfs(n-1, parent_k)
res = dfs(n, k)
return 0 if res else 1