Cheapest flights within k stops

Link: https://leetcode.com/problems/cheapest-flights-within-k-stops/

Solution:

Topics: BFS, Dijkstra’s

Intuition
The optimized BFS solution is quite clear to me, but the modified Dijkstra’s far less so. In any case, I’ll include both implementations and will devote more attention to Dijkstra’s on future revisions.

It’s hard to imagine that this problem is anything other and optimized BFS or Dijkstra’s because we are dealing with a weighted graph here (the weights are flight costs). Optimized BFS comes to mind, as we can revisit nodes opportunistically should the running cost be lower than what’s in our cache.

Implementation (BFS)

def cheapest_flights(n, flights, src, dst, k):
	adj = {city:[] for city in range(n)}
	for from_city, to_city, price in flights:
		adj[from_city].append((to_city, price))
 
	res = -1
	costs = {}
	queue = deque([(src, 0, 0)])
	while queue:
		city, flights, cost = queue.popleft()
		if flights > k + 1:
			continue
		if city in costs and cost >= costs[city]:
			continue
		costs[city] = cost
		if city == dst:
			res = cost
 
		for to_city, price in adj[city]:
			queue.append((to_city, flights+1, cost + price))
	return res
			
 
#time: o(e*k) because we could traverse each edge maximum K times
#memory: o(e*k) hold all e*k traversals in the queue

The Dijkstra’s approach is way less clear to me and its actually a bit less efficient than the above (at least according to the leetcode editorial). The idea is to greedily explore the lowest cost path, and proactively prune explorations BEFORE they enter the queue (heap in the case of Dijkstra’s). If either the cost is lower than the cached cost or the number of stops is lower than the cached number of stops…we allow the exploration.

Implementation (dijkstra’s)

def cheapest_flights(n, flights, src, dst, k):
	adj = {city:[] for city in range(n)}
	for from_city, to_city, price in flights:
		adj[from_city].append((to_city, price))
	stops = {city: float('inf') for city in range(n)}
	costs = {city: float('inf') for city in range(n)}
	stops[src] = 0
	costs[src] = 0
 
	min_heap = [(0, 0, src)]
	while min_heap:
		cost, flights, city = heappop(min_heap)
		if flights > k + 1:
			continue
		if city == dst:
			return cost
 
		for to_city, price in adj[city]:
			new_cost = cost + price
  			if flights + 1 < stops[to_city] or new_cost < costs[to_city]:
	  			stops[to_city] = flights + 1
	  			costs[to_city] = new_cost
				heappush(min_heap, (new_cost, flights + 1, to_city))
	return -1

Mnemonic
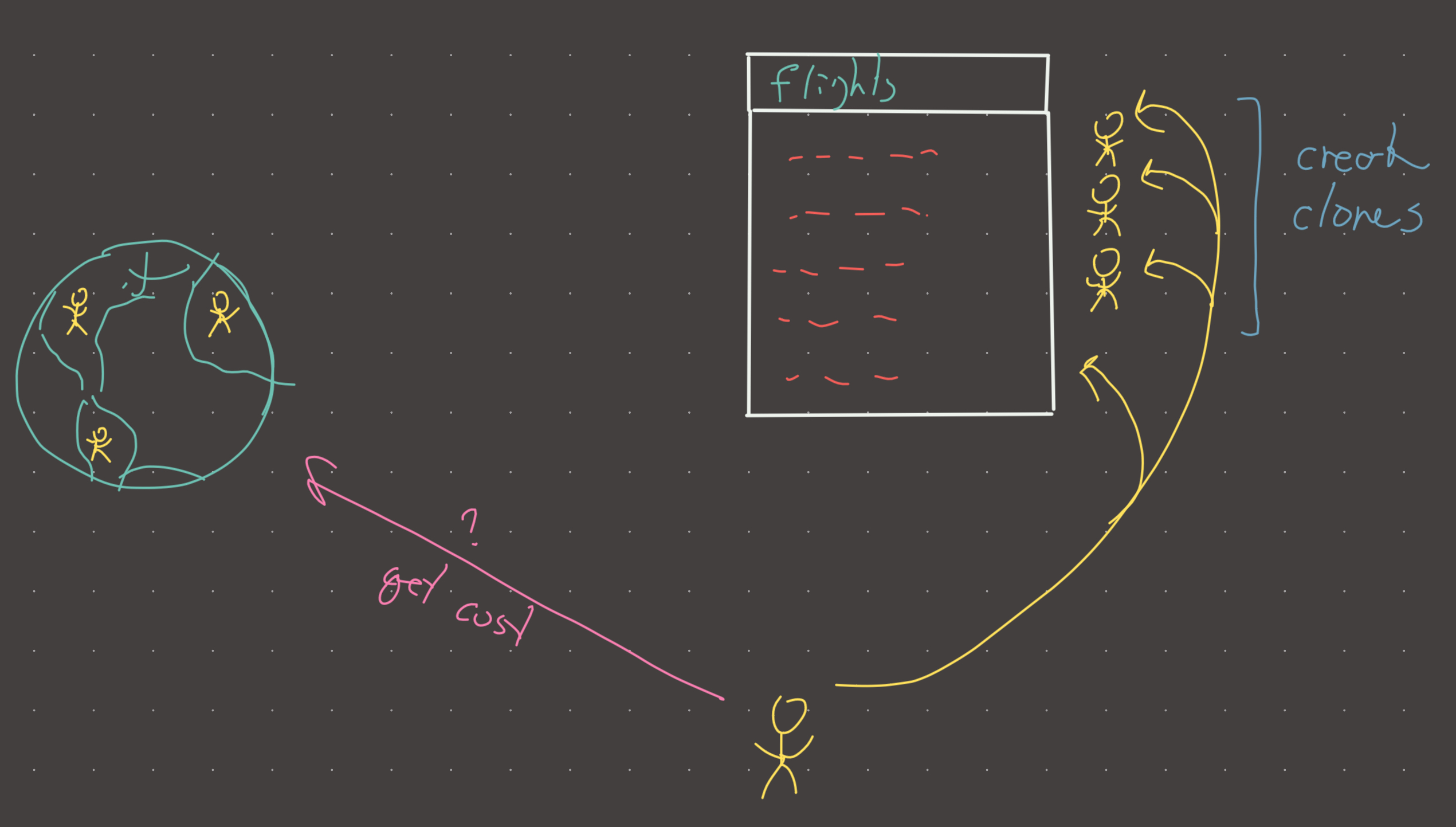
At airport. Clone myself to take every available flight to every possible city…but first call all my clones (or siblings?!) and ask if we had already been to that city (if yes, get the cost), and only create a new clone to go to that city if I get there at less cost.

Visual

Review 1
The main insight for this problem is that we must keep track of stops as well as costs. Its pretty obvious that costs must be tracked because we want to disallow visiting the same nodes with a higher cost…this part is standard optimized BFS or Dijkstra’s. This problem is more complicated however. Why? Because there is a constraint on the length of the path! There must be no more than K stops. Simple right? Just put a hard constraint on path_len? Not so fast.

What if the cost of visiting the node again is the same, but the number of stops is lower than the last time around? Do we still explore? Yes! What if the cost is higher but the number of stops is lower? We also explore! Both of these cases could potentially lead to a lower end cost for reaching the destination!

The last edge case to consider is how we count stops. We want to make sure that we are not counting the level, or even the number of edges! The number of stops will in fact be the number of nodes in the path minus two. Why? This is the case because we don’t count the start or the destination:

a-b-c   ---> 1 stop (3-2)
  ^

a-b-c-d-e ---> 3 stops (5-2)
  ^ ^ ^

We must account for this in our stopping logic. It would seem that counting cities is the way to go here but this has too many edge cases because we can only discount the last city when we get to it, so its better to just start at zero and add stops as we need them (making sure to check if we are at our destination before adding a stop).

review