Count primes

Link: https://leetcode.com/problems/count-primes/

Solution:

Topics: math, Sieve of Eratosthenes

Intuition
This problem uses a cool ancient algorithm called the Sieve of Eratosthenes. Conceptually, this algorithm finds primes by process of elimination. We know that the first prime is 2, so we know any multiply of 2 between 2 and n is NOT a prime (primes are only divisible by 1 and themselves). So essentially, we mark non-primes and then move to the next prime…which in the case of 2 is 3.

For example:

n = 10

initialize a boolean list that represents the state (prime or not prime) of all integers between 0 and 10 (exclusive). We include the zero because we want the indices to represent the integers. 

The first two indices are 0 and 1, and neither are primes so we just initialize them as false.

primes = [False, False, True, True, True, True, True, True, True, True]
                        

						
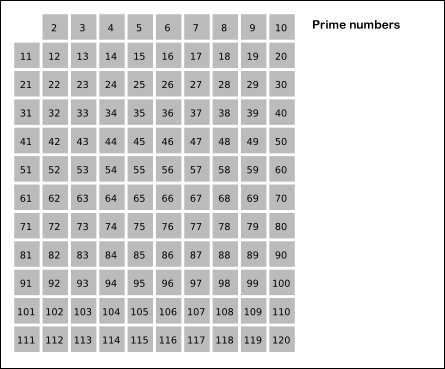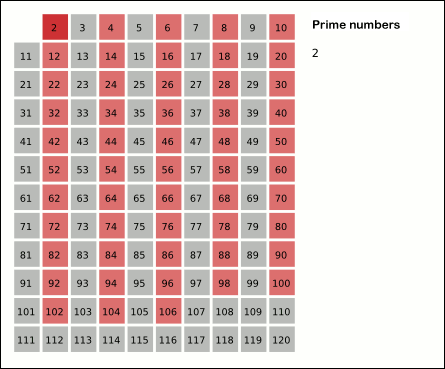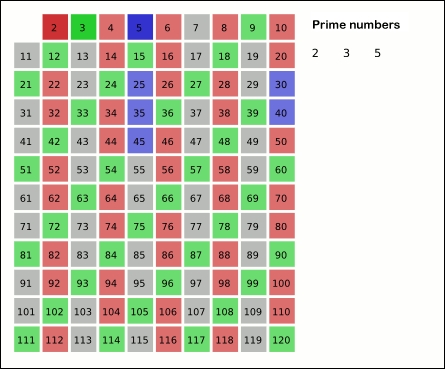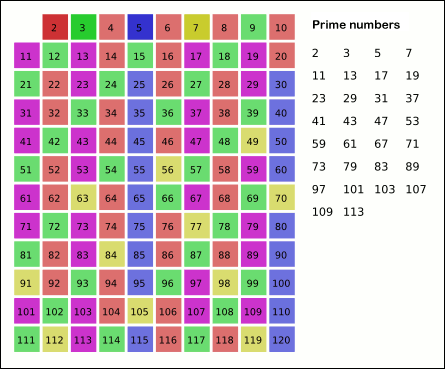
So we move to the first prime index 2 (first True from the left), and set all multiples of 2 to False, as 2, 6, 8 are composite numbers. 

primes = [False, False, True, True, False, True, False, True, False, True]
                        ^           *            *            *


Move to the next prime (3) and set all multiples of 3 to False (6, 9)

primes = [False, False, True, True, False, True, False, True, False, False]
                              ^                  *                   *


Move to the next prime (5), all multiples are out of range.

primes = [False, False, True, True, False, True, False, True, False, False]
                                           ^


Move to the next prime (7), all multiples are out of range. 

primes = [False, False, True, True, False, True, False, True, False, False]
                                                        ^


So, we have 2,3,5,7 as all the primes smaller than 10, which is correct.

There are a couple optimizations here. Firstly, we don’t need to do this for all n numbers. We can actually early exit at sqrt(n), because all composite numbers at that point would have already been marked.

Another minor optimization is to start the inner loop at p*p instead of p+p. I don’t really understand why this is the case, but practically speaking all numbers between p and p*p would have already been marked by previous primes so we can start directly at p*p.

The last optimization is how to actually compute the result, because the problem statement ask for the number of primes, not the primes themselves. Since we have a boolean list, a neat way to do this is to take the sum of the list! False evaluates to zero and True evaluates to 1. Also sum(x) in python is much faster than looping because that function is written in C.

Implementation

def count_primes(n):
	if n < 3:
		return 0
	primes = [True]*n
	primes[0] = False
	primes[1] = False
	i = 0
	while i < sqrt(n):
		if primes[i]:
			p = i*i
			while p < n:
				primes[p] = False
				p += i
		i += 1
	return sum(primes)
 
#time: o(sqrt(n)log(n))
#memory: o(n)

Visual

Review 1
Very cool problem. Even the second time around I was completely stumped! But I did remember that I had to use the Sieve of Eratosthenes, I just could not remember what it actually was! After re-reading the wiki, I was able to implement it but missed a couple optimizations.

Basically this is a process of elimination, so we create a list of True of length n…this is how we will flag elements in n as primes or not. We initialize all to True because we will go about eliminating them, and at the end of the algorithm, the sum will be the number of primes (because True evaluates as 1 in arithmetic operations)!

So we don’t know what a prime is…in fact we have no way to compute them directly, but we do know what is not a prime. A number that is not a prime will be a composite of some other numbers. So the idea here is to start at a prime number (2 is the first), and mark all multiples of 2 as not primes! Move on to the next number whose flag is still True (in this case 3), repeat the process! Do this for all numbers up to n, and in the end only the numbers whose flags have not been flipped are primes!

Now, n can be large, so do we have to do this for every number up until n? NO! We can stop at sqrt(n). Why? Since we start the next prime at i*i, it means that once we reach sqrt(n), we have already reached n and have no more primes to count!

review
hard