Count the number of good subarrays

Link: https://leetcode.com/problems/count-the-number-of-good-subarrays/

Solution:

DSA: sliding window, hash map, subarray

Intuition
The problem is kind of tricky, but really what it’s asking is for the number of pairs of duplicates in the subarray.

Lets say we have a frequency map of the numbers so far and we have reached the number 2. It just so happens that the number 2 was already seen 3 times. This means that that the 2 that we are seeing creates 3 more pairs with the ones that have been seen previously (one for each).

So as we iterate forwards through the list, we keep a frequency map and if the number has been seen previously, we add freq[current] to the number of pairs for the window.

While curr_pairs is greater or equal to K, run a while loop to shrink the window until curr_pairs is smaller than K. Now we add the value of the left pointer (L) to the result. Why?

For example take:
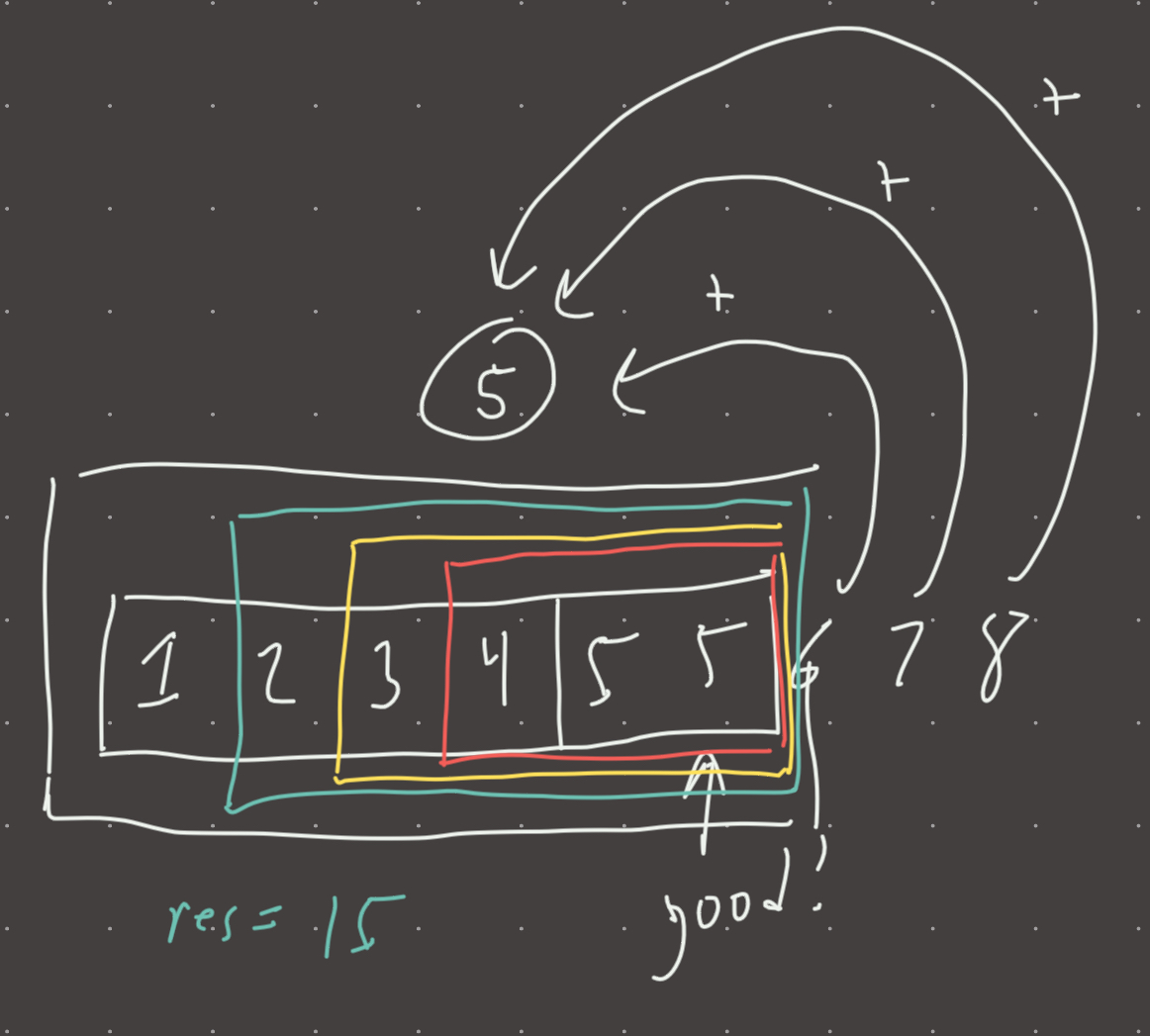
[1,2,3,4,5,5] and K = 1

1. we see that the only pair is [5,5] but our sliding window, would be L=0 and R=5 when K = 1
2. but we must also count every subarray that can be MADE with [5,5]!
3. namely [4,5,5], [3,4,5,5], [2,3,4,5,5], and [1,2,3,4,5,5]!
4. the convenient way to do this is just add L to the result after sliding the window over until curr_pairs < k . After doing this, our window ends up at L=5, R=5, so we add 5.
5. This represents all subarrays that can be made with all elements up until the leftmost.
6. The answer is indeed 5: [5,5], [4,5,5], [3,4,5,5], [2,3,4,5,5], and [1,2,3,4,5,5]!

There is one notable “mind-fuck”. If we do res += l after the while loop, wouldn’t we be adding to the result at every iteration? Yes. Why?

For example, what if we had:
[1,2,3,4,5,5,6] and K = 1

1. We see that like the previous problem, we have one pair, but the complication is that we have a 6 at the end which can form 5 more good subarrays : [5,5,6], [4,5,5,6], [3,4,5,5,6], [2,3,4,5,5,6], and [1,2,3,4,5,5,6]
2. We can see that it formed precisely 5 more, so adding L again on 6 actually works.
3. Think of L as a RESERVOIR for for the good subarrays up until that point, and each element in the future adds everything in the reservoir to the result.

Implementation

def countGood(self, A: List[int], k: int) -> int:
	res = 0
	counts = {}
	l = 0
	current_pairs = 0
	for r in range(len(A)):
		if A[r] in counts:
		current_pairs += counts[A[r]]
		counts[A[r]] = counts.get(A[r], 0) + 1
		while current_pairs >= k:
			counts[A[l]] -= 1
			current_pairs -= counts[A[l]]
			l += 1
		res += l
	return res

Visual

Review 1
A sliding window with a frequency map will keep track of the number of pairs. Shrink the window while curr_pairs >= k to get the number of subarrays that can be formed in the left partition. The key point is that more subarrays can be formed with the right partition, so we must count those too as we shrink the window.

In the above case, 5 subarrays can be formed in the left partition and 3 contiguous subarrays are in the right partition. So how many subarrays can be formed? 3*5!

Consider both left and right partitions, and multiply them!

Implementation (Review 1)

	res = 0
	counts = {}
	l = 0
	current_pairs = 0
	for r in range(len(A)):
		if A[r] in counts:
		current_pairs += counts[A[r]]
		counts[A[r]] = counts.get(A[r], 0) + 1
 
		good_left = 0
		while current_pairs >= k:
			good_left += 1
			counts[A[l]] -= 1
			current_pairs -= counts[A[l]]
			l += 1
		right = len(A)-r
		res += good_left*right  #this implementation is more intuitive. 
	return res

review