Link: https://leetcode.com/problems/number-of-valid-subarrays/
Solution:
DSA: monotonic stack, subarray
Intuition
Tricky problem, but the solution is quite simple with a monotonically increasing stack. If we keep a monotonically increasing stack, the length of that stack at every iteration is exactly how many valid subarrays can be formed. Somewhat similar to Count the number of good subarrays, in terms of using a RESERVOIR, but here our reservoir is the length of the stack!
Why is this the case? Because consider the array [1, 2, 3, 0]. After adding 1 to the stack our stack is [1]. The stack is monotonic, so we add 1 to our result which corresponds to the subarray [1].
Next we add 2 and get [1, 2], the stack is still monotonic so we add 2 to the result which corresponds to the subarrays [1, 2] and [2].
Next we add 3 and get [1, 2, 3], the stack is still monotonic so so so we add the 3 to the result (length of the stack) which corresponds to the subarrays [3], [2, 3] and [1, 2, 3].
Next we add 0 and get a stack of [0] because 0 pops off everything that is greater than it to retain the monotonically increasing property. So now we add 1 to the result because the length of the stack is now 1 which corresponds to the subarray [1]
The key to this problem is understanding that every element that we add to the stack can form another valid subarray with every element that already exists on the stack (including itself).
Implementation
def valid_subarrays(nums):
res = 0
stack = []
for num in nums:
while stack and stack[-1] > num:
stack.pop()
stack.append(num)
res += len(stack)
return res
Visual
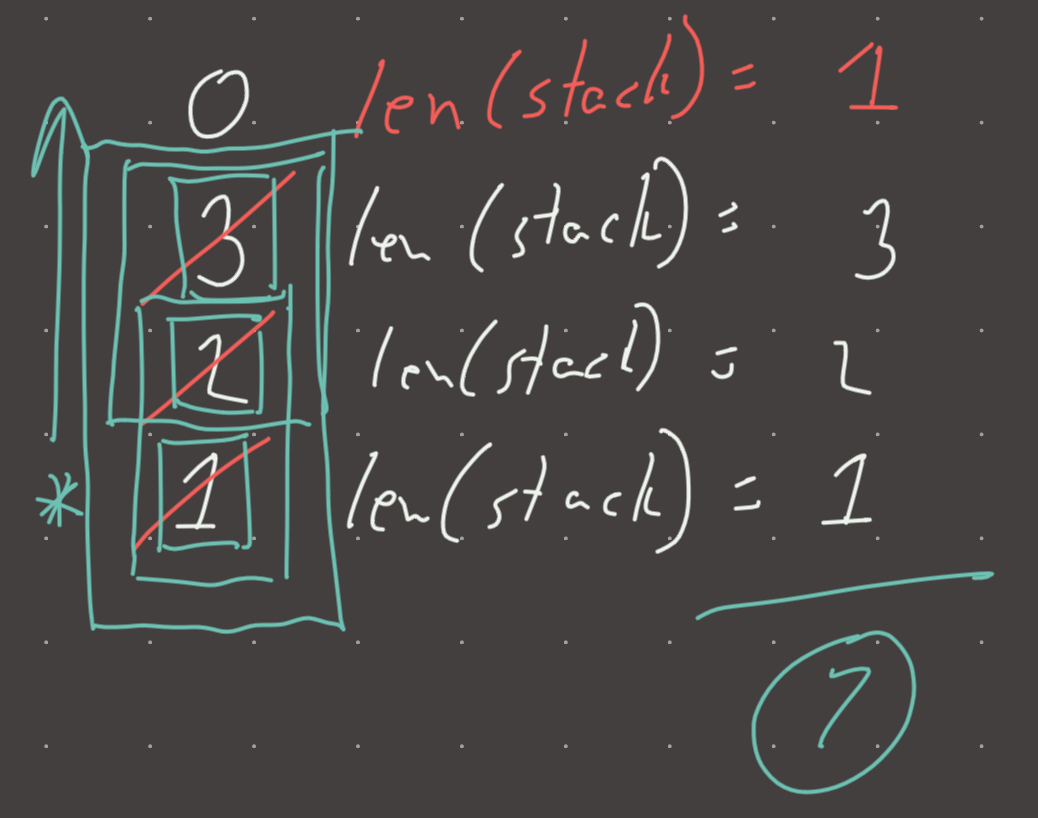
Review 1
Very quickly I understood to use a monotonic stack but I spent a little bit of time figuring out how to count the subarrays correctly. Basically, we find the next smaller number using an increasing monotonic stack and the length of the subarray right before number that did the popping is added to the result. Numbers that do not get popped have valid subarrays that extend to the end of the list so handle them accordingly.
This is different from the approach that I have described above but I think it’s more intuitive to use the indices directly. The above implementation is equivalent to holding a reservoir, but it’s a bit too clever and not very generic. This code is longer but more intuitive IMO.
Next greater element II
Sliding window maximum
Implementation (Intuitive)
def val_sub(nums):
res = 0
stack = []
for i, num in enumerate(nums):
while stack and num < stack[-1][0]:
_, index = stack.pop()
length = i - index
res += length
stack.append((num, i))
while stack:
_, index = stack.pop()
res += len(nums) - index
return res